Zahlenraten

Wir schauen und das "Zahlenraten" Beispiel genauer an:

	Zahlenraten: Deine Freundin denkt sich eine zahl zwischen 1 und 100, du musst die Zahl mit möglichst wenigen Versuchen erraten. Die Freundin sage dir jeweils, ob die geratene Zahl zu groß, zu klein oder richtig ist.
1)

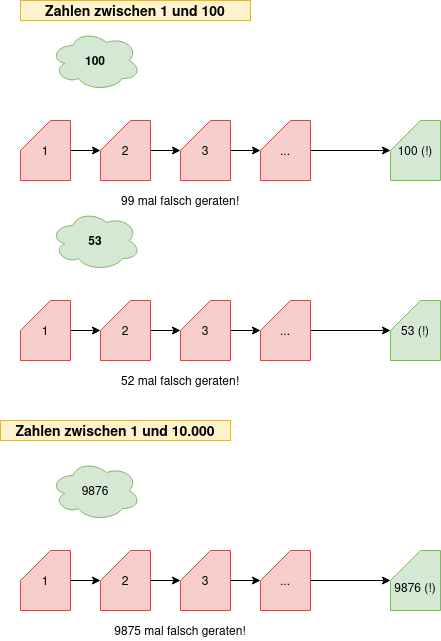
Ziel ist natürlich, die Zahl mit möglichst wenigen Versuchen zu erraten. Wenn du einfach bei 1 beginnst und "hochzählst", ist das allerdings unter Umständen schlecht: Wenn deine Freundin sich die Zahl 100 gedacht hast, rätst du 99 mal falsch. Der "Worst Case" für dieses Verfahren ("Der Reihe nach raten") benötigt also 100 Versuche, um die Zahl sicher zu finden.

Es kann auch mal weniger Versuche benötigen, aber im ungünstigsten Fall - 100 Versuche. Wenn ihr die Spielregeln nun ändert, und die gedachte Zahl zwischen 1 und 10.000 liegen darf, benötigst du mit "Der Reihe nach raten" um schlechtesten Fall sogar 10.000 Versuche!

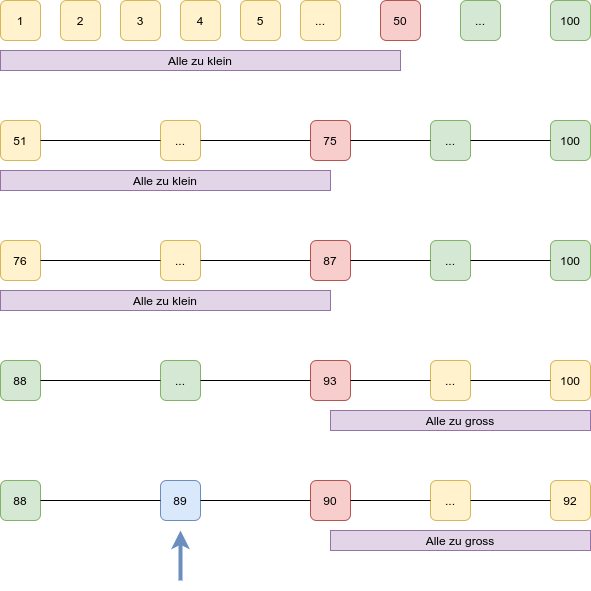
Zurück zum Beispiel - Zahlen von 1 bis 100. Geschickter wäre es, wenn man als erste Zahl 50 wählen würde, denn damit hat man mit einmal raten die Hälfte aller Möglichkeiten eliminiert - erinnert euch daran, dass die Antwortmöglichkeiten der Freundin "zu klein", "zu groß" oder "Treffer" sind. Wenn die gedachte Zahl 89 ist, erhält man die Information "zu klein" und kann alle Zahlen kleiner als 50 ebenfalls als Möglichkeiten ausschließen.

Im nächsten Schrittt wählt man nun die Mitte der verbleibenden Möglichkeiten, als des Bereichs zwischen 51 und 100 – 75, und erhält wieder die Rückmeldung "zu klein". Nun weiß man, dass die gesuchte Zahl zwischen 76 und 100 liegt. Und so weiter - das sieht dann so aus:

Nach 5 mal Raten weiß man das Ergebnis.

Wäre die gedachte Zahl 87 gewesen, hätte man das Ergebnis schon nach 3 Schritten gehabt (man kann auch immer mal Glück haben) - aber wie lange hätte es höchstens gedauert? Hier hilft es, sich klarzumachen, wieviele Zahlen nach jedem Rateversuch bei diesem Verfahren noch als Kandidaten im Rennen sind, ohne an eine spezielle Zahl zu denken:

• (1) Nach wievielen Rateversuchen ist man im schlechtesten Fall erfolgreich, wenn man eine Zahl zwischen 1 und 10.000 mit der binären Suche erraten möchte. Schätze zuerst, überlege dann.

• (2) Du suchst in einem Wörterbuch mit 320.000 Wörtern nach einem zufälligen Begriff. Wieviele Schritte benötigst du im ungünstigsten Fall mit der einfachen Suche (der Reihe nach) und der binären Suche?

• (3) Wie viele Versuche benötigt man bei der binären Suche in einer sortierten Liste mit n Elementen allgemein im schlechtesten Fall, um das gesuchte Element zu finden?

• (4) Erkläre, warum die binäre Suche in unsortierten Listen nicht funktionieren kann.

Einführung <<<< – Zahlenraten – >>>> Ein Programm