Inhaltsverzeichnis

Der Call-Stack und die Rekursion

Ein populäres Beispiel für rekursive Algorithmen ist die Fakultätsfunktion: 

5! = 5*4*3*2*1
fakultaet(5) = 120
fakultaet(3) = 3*2*1 = 6

(A1) Iterativ

Implementiere in BlueJ eine iterative Version der Fakultätsfunktion, die als Argument die Zahl entgegennimmt, deren Fakultät berechnet werden soll.

(A2) Rekursiv

Implementiere anhand des folgenden Pseudocodes eine rekursive Version fak_rekursiv. 

fak_rekursiv(int n):
  wenn n=1 oder n=0: 
    return 1
  sonst:
    return n*fak_rekursiv(n-1)

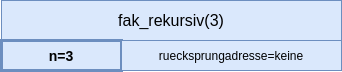
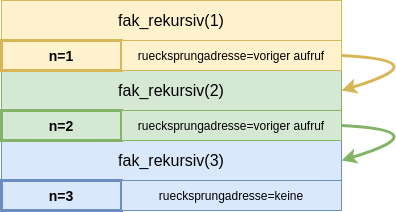
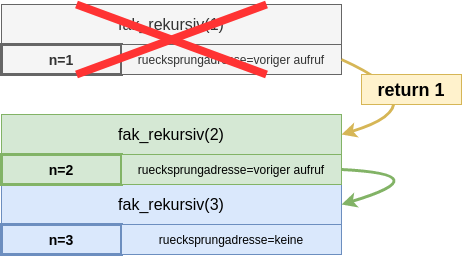
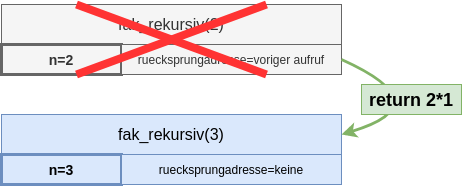
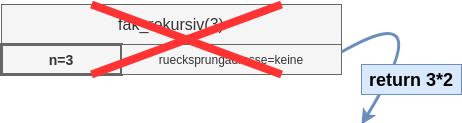
Dataillierte Betrachtung des Call-Stacks bei der Rekursion

Was passiert Wie sieht der Stack aus?

fak_rekursiv(3) wird aufgerufen.
Auf dem Stack wird Speicher für diesen Aufruf reserviert. Es gibt keine Rücksprungadresse.
Innerhalb dieses Aufrufs wird fak_rekursiv(2) (nächster Schtritt) aufgerufen,
da die Fallunterscheidung nicht zum Basisfall
führt sondern zum Rekursionsfall.

fak_rekursiv(2) wird aus dem vorhergehenden Aufruf heraus aufgerufen.
Auf dem Stack wird Speicher für diesen Aufruf reserviert: Wichtig: Jeder Aufruf
hat seinen eigenen Speicherbereich
für Variablen, d.h. jeder Aufruf
von fak_rekursiv hat sein eigenes n auf die die anderen Aufrufe
nicht zugreifen können.
Die Rücksprungadresse befindet sich jetzt im vorigen Aufruf
der rekursiven Methode selbst.
Das ist anders, als beim ersten Beispiel für den Call-Stack!
Da erneut der Rekursionsfall eintritt,
wird aus diesem Aufruf heraus fak_rekursiv(1) aufgerufen.

fak_rekursiv(1) wird aus dem vorhergehenden Aufruf heraus aufgerufen.
Auf dem Stack wird Speicher für diesen Aufruf reserviert.
Die Rücksprungadresse befindet sich wiederum im vorigen Aufruf der rekursiven Methode selbst.
Jetzt tritt der Basisfall ein!

Dies ist der erste Aufruf, der vollständig abgeschlossen ist.
Es wird kein neuer Aufruf von fak_rekursiv auf den Call-Stack gelegt, sondern
der Aufruf von fak_rekursiv(1) endet damit, dass 1 an die
aufrufende Stelle zurückgegeben wird und die zum Aufruf gehörenden
Daten vom Stack entfernt werden.

Damit hat der Aufruf von fak_rekursiv(2) alle Informationen,
um abgeschlossen zu werden:
Der Ausdruck n*fak_rekursiv(n-1) kann jetzt zu 2*1 ausgewertet und an die
aufrufende Stelle zurückgegeben werden.
Die zum Aufruf gehörenden
Daten werden vom Stack entfernt.

Jetzt hat auch der Aufruf von fak_rekursiv(3) alle Informationen,
um abgeschlossen zu werden:
Der Ausdruck n*fak_rekursiv(n-2) kann jetzt zu 3*2 ausgewertet
und an die aufrufende Stelle zurückgegeben werden.
Die zum Aufruf gehörenden Daten werden vom Stack entfernt.
Der Call-Stack ist leer, der Aufruf der Methode beendet.

Zusammenfassung

  • Rekursion bedeutet, dass eine Funktion/Methode sich selbst aufruft.
  • Alle rekursiven Funktionen haben eine Fallunterscheidung: den Basisfall und den Rekursionsfall.
  • Die Funktionsaufrufe werden auf dem Aufruf-Stack gespeichert, dabei wird dieser immer größer bis der Basisfall eintritt. Anschließend wird der Stack von oben nach unten "abgearbeitet", bis er leer ist und damit der Aufruf der rekursiven Methode endet.
  • Der Aufruf-Stack kann unter Umständen sehr groß werden und sehr viel Arbeitsspeicher belegen.