Mergesort

Mergesort und Quicksort sind essentielle Bestandteile der heutigen informationstechnologischen Infrastruktur - ohne diese beiden Algorithmen sähe die Welt anders aus, da praktisch alle IT Systeme ständig Daten sortieren müssen.

• Mergesort kommt beispielsweise zum Einsatz bei Java-Methoden zum Sortieren von Objekte, sortieren in Perl, stabile Sortierverfahren bei CPP und Python, JavaScript Implementation von Firefox. Mergesort war einer der ersten in den 1940er Jahren auf dem EDVAC ausgeführten Algorithmen.
• Quicksort ist die Basis beim Sortieren von primitiven Typen in Java, qsort bei C, Visual C, Python, Matlab und JavaScript in Chrome basierten Browsern.

Mergesort ist eine Divide-and-Conquer¹⁾ Algorithmus, der prinzipiell folgendermaßen funktioniert:

• Teile das Array in zwei Hälften (Divide).
• Sortiere (rekursiv) die beiden Hälften (Sort).
• Füge die beiden Hälften wieder zu einem sortierten Array zusammen (Merge / Conquer).

Bevor wir den gesamten Algorithmus betrachten, wollen wir uns zunächst nur mit dem Schritt des korrekten Zusammenfügens zweier sortierter Teilarrays zu einem sortierten Array beschäftigen, denn dort findet die eigentliche "Sortierarbeit" bei MergeSort statt.
Wir schauen also an einem Beispiel nochmal etwas genauer, wie man diesen Vorgang verstehen und implementieren kann.

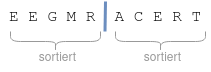
Gegeben sind zwei sortierte Teilarrays, die zu einem sortierten Array zusammengefügt werden sollen:

Dazu gehen wir wie folgt vor:

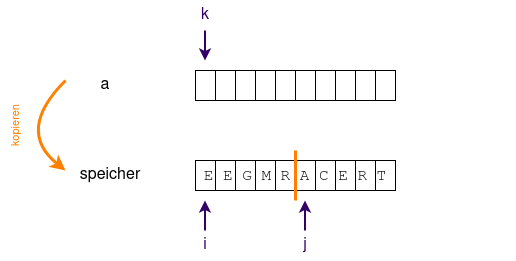
• Zunächst kopieren wir das gesamte Array in ein "Speicherarray".
• Anschließend verwenden wir drei Indizes:
  • i: Beginnt beim ersten Element des ersten Teilarray des Speicherarrays
  • j: Beginnt beim ersten Element des zweiten Teilarrays im Speicherarray
  • k: Beginnt beim ersten Element des Arrays, das zusammengesetzt werden soll

i und j laufen jetzt durch die Teilarrays, die zugehörigen Elemente werden verglichen. Das kleinere der beiden Elemente wird ins ursprüngliche Array übernommen und der jeweilige Index inkrementiert. Gelangt ein Index ans Ende, kann der Rest des unvollständig abgearbeiteten Teilarrays übernommen werden.

Implementiere im Bluej-Projekt https://codeberg.org/qg-info-unterricht/algs4-sort-bluej in der Klasse StandaloneMerge das Zusammenführen der beiden Teilarrays a und b in der Methode merge() (ohne Parameter). Die Hinweise sind gestufte Hilfen, die du bei Problemen nacheinander ansehen kannst.

Hinweis 1:

Hinweis 2:

merged = new String[a.length + b.length]; 
 
// Das sind die Indizes für die beiden Teilarrays
// Beide beginnen bei 0
int ia = 0; // Zeiger auf das Element in Teilarray a
int ib = 0; // Zeiger auf das Element in Teilarray b
 
 
// im läuft von 0 bis merged-length-1
// bei jedem Durchlauf muss ein neues Element eingefügt werden -
// nur welches?     
// Es müssen 4 Fälle unterschieden werden. Denke an die Länge der Arrays a und b!
for(int im=0; im<merged.length; im++) {
 
// Fall 1:
 
// Fall 2:
 
// Fall 3: 
 
// Fall 4: 
 
}

Hinweis 3:

merged = new String[a.length + b.length]; 
 
// Das sind die Indizes für die beiden Teilarrays
// Beide beginnen bei 0
int ia = 0; // Zeiger auf das Element in Teilarray a
int ib = 0; // Zeiger auf das Element in Teilarray b
 
// im läuft von 0 bis merged-length-1
// bei jedem Durchlauf muss ein neues Element eingefügt werden -
// nur welches?     
// Es müssen 4 Fälle unterschieden werden. Denke an die Länge der Arrays a und b!
for(int im=0; im<merged.length; im++) {
 
// Fall 1 und 2 müssen überprüfen, ob sich die 
// Indizes von a und b im erlaubten Bereich befinden.
// Was bedeutet das, wenn der Index außerhalb des erlaubten Bereichs ist?
// Was muss dann geschehen? 
 
  // Fall 1: ia ist außerhalb der Länge von a
  if(ia >= a.length) {
 
  // Fall 2:  ib ist außerhalb der Länge von b           
  } else if(ib >= b.length) {
 
  // Fall 3:              
  } else if() {
 
  // Fall 4:          
  } else {
 
  }    
}

Hinweis 4:

merged = new String[a.length + b.length]; 
 
int ia = 0; // Zeiger auf das Element in Teilarray a
int ib = 0; // Zeiger auf das Element in Teilarray b
 
for(int im=0; im<merged.length; im++) {
  if(ia >= a.length) {
    // Das Array a ist abgearbeitet, jetzt können die Elemente 
    // von b ohne weiteres nach merged übertragen werden, weil a und b
    // ja sortiert sind! Der Index von b muss jeweils erhöht werden.
    merged[im] = b[ib];
    ib++;
  } else if(ib >= b.length) {
    // Das Array b ist abgearbeitet, jetzt können die Elemente 
    // von b ohne weiteres nach merged übertragen werden, weil a und b
    // ja sortiert sind!
    merged[im] = a[ia];
    ia++;
  } else if(less(b[ib], a[ia])) {
    // Was fehlt hier? 
  } else {
    // Was fehlt hier?        
  }    
}

Lösungsvorschlag

merged = new String[a.length + b.length]; 
 
int ia = 0; // Zeiger auf das Element in Teilarray a
int ib = 0; // Zeiger auf das Element in Teilarray b
 
// im zeigt auf das zu besetzende Element im gemergten Array merged
for(int im = 0; im < merged.length; im++) {
   // a ist schon komplett in merged - kopiere die Elemente von b
   if(ia >= a.length) { 
       merged[im] = b[ib];
       ib++;
   } else if (ib >= b.length) { // b ist schon komplett in merged - kopiere Elemente von a
       merged[im] = a[ia];
       ia++;
   } else if(less(a[ia],b[ib])) { // a[ia] ist das aktuell kleinere - kopiere nach merged
        merged[im] = a[ia];
        ia++;
    } else { // b[ib] ist kleiner - kopiere nach merged
        merged[im] = b[ib];
        ib++;
    }
 
}

Nachdem wir jetzt über eine funktionale Methode zum Zusammenfügen der Teilarrays verfügen, implementieren wir den gesamten Algorithmus, inklusive der rekursiven Aufrufe.

Implementiere unter Verwendung der oben implementierten merge-Methode einen naiven Mergesort-Algorithmus in der Methode public String[] msort(String[] a). Eine Vorlage findest du im Bluej-Projekt https://codeberg.org/qg-info-unterricht/algs4-sort-bluej in der Klasse MergeSortNaiv. Eine Methode public String[] merge(String[] s, String[] t) ist entsprechend bereits implementiert.

Orientiere dich an folgendem Pseudocode:

msort: String[] a
  wenn a.laenge ist 1: 
    return a
  ende wenn
  
  mitte = a.lange/2
  
  ta1=teilarray von a von 0 bis mitte-1
  ta2=teilarray von mitte bis a.laenge-1
  
  return merge(msort(ta1), msort(ta2))

• Teste den Algorithmus
• Bewerte die Implementation in Hinsicht auf Ressourcenverbrauch und Effizienz

Lösungsvorschlag

// Mergesort naiv
    public String[] msort(String[] a) {
        // Implementiere hier gemäß des Pseudocodes im Wiki
        if(a.length == 1) {
            return a;
        }
 
        int mitte = a.length/2;
        // Dieser Schritt ist aufwändig!
        // Man muss Arrays erzeugen und alle Elemente 
        // in die neuen Teilarrays hineinkopieren.
        // das ist O(n) bei jedem Aufruf :(
        String[] ta1 = new String[mitte];    
        String[] ta2 = new String[a.length-mitte];
        for(int i=0; i<mitte; i++) {
            ta1[i]=a[i];
        }
        for(int i=mitte; i<a.length;i++) {
            ta2[i-mitte] = a[i];
        }
        return merge(msort(ta1),msort(ta2));
    }

(A) Der folgende Aufrufbaum stellt dar, wie das Array String[] a = { "9", "4,", "3", "8", "1"} sortiert wird.

• In welcher Reihenfolge finden die Aufrufe der Funktion msort statt?
• An welchen Stellen im Baum wird ein merge-Vorgang ausgelöst?

Lösung

(B) Gegeben ist der folgende String, der sortiert werden soll: String[] a = {"F", "Z", "K", "A", "C" }. Zeichne einen Aufrufbaum für diesen Vorgang.

Gib zunächst getrennt den Aufwand der Splitphase und der Mergephase in O-Notation an und begründe deine Aussage. Überlege dann, wie daraus abgeleitet der generelle Aufwand für den gesamten Mergesort-Algorithmus ist.

Prinzipiell funktioniert unser "naiver Mergesort", jedoch ist die häufig auftretende Operation der Arrayerzeugung und das Hineinkopieren der Array-Elemente beim Teilen des Arrays teuer und sollte vermieden werden.

Wir befassen uns zunächst nochmal mit dem Merge-Vorgang und implementieren mit unseren Kenntnissen vom ersten Versuch die Methode

  public void merge(String[] a, String[] speicher, int min, int mitte, int max) 

in der Klasse StandaloneMerge. Um diese Methode aufrufen zu können, müssen wir die beiden Arrays a und b im Konstruktor zusammenfügen und außerdem ein Speicherarray derselben Länge erzeugen, das man dem Methodenaufruf mitgeben kann.

• Vollziehe das Zusammenfügen der Arrays, das Erzeugen des Speicher-Arrays und die Bestimmung den Methodenparameter nach.
• Entferne die Kommentarzeichen vor dem Methodenaufruf im Konstruktor.

Der "Kniff" ist später, dass man das Speicher-Array vor den rekursiven Aufrufen nur einmal erzeugt und dann mit den Parametern min, mitte und max steuert, welche Bereiche des Arrays zusammengefügt werden sollen. So muss man nicht in der Rekursion neue Arrays erzeugen, wie beim naiven Ansatz.

Es ist also wichtig, beim Übertragen der Elemente ins Speicher-Array in der merge Methode bei min zu beginnen und bei max zu enden, ebenso wie die beiden Indizes i und j bei min und bei mitte+1 beginnen:

public void merge(String[] a, String[] speicher, int min, int mitte, int max) {
 
        // Übertragen der Elemente von min bis max in 
        // das bereits vorhandene Speicherarray
        for(int i=min; i<=max;i++) {
            speicher[i]=a[i];
        }
 
        int i=min;
        int j=mitte+1;
 
        for(int k=min; k<=max; k++) {
         // Die vier Fälle von oben
        }
 
        System.out.print("In einem Speicherarray: ");
        System.out.println(Arrays.toString(a));
    }

Vervollständige die Implementierung, indem du die vier Fälle passend in die neue Methode überträgst.

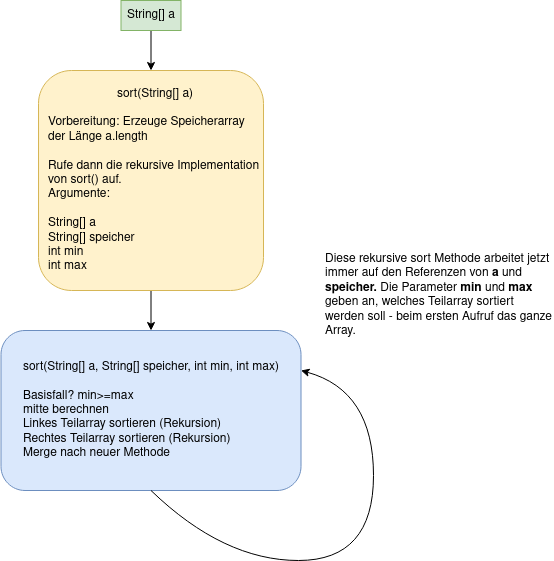
Unter Verwendung der neuen Merge-Methode können wir jetzt eine Mergesort Implementation erzeugen, die nicht in jedem Rekursionsschritt neue Arrays erzeugen muss.

Im BlueJ-Projekt findest du eine Methode MergeSort, in der dieses Vorgehen vorbereitet ist. Vervollständige die Implementation.