Um Abläufe einheitlich und verständlich mit Hilfe von Automaten darstellen zu können, ist es nötig, eine einheitliche Notation (Zeichen, Symbole, Schreibung) für Automaten zu verwenden. Diese lernst du im folgenden Kapitel kennen. Dabei werden die Begriffe Zustand, Übergang und Eingabe von Automaten erläutert. Außerdem wird das Verhalten von Automaten auf Aktionen genauer betrachtet.

Nach der Bearbeitung dieses Kapitels kannst du…

• unterscheiden, was in der Automatentheorie unter den Begriffen Zustand, Übergang, Eingabe und Reaktion zu verstehen ist.
• Zustände und Übergänge in exemplarischen, graphischen Darstellungen benennen.
• bestimmen, in welchem Zustand sich ein Automat nach einer bestimmten Eingabe befindet.
• das Eingabealphabet eines Automaten bestimmen.

Automaten kann man sich als eine Art "Maschine" vorstellen, die stur einem festgelegten Schema folgt, so wie zum Beispiel eine Kaffeemaschine. Eine Kaffeemaschine kann sich in verschiedenen Zuständen befinden (warten, Kaffee kochen, Kaffee warmhalten). Das festgelegte Schema sagt ihr, dass sie, wenn sie angeschaltet wird, Kaffee kochen soll. Wenn sie damit fertig ist, soll sie den Kaffee warmhalten, solange bis sie ausgeschaltet wird.

Im Allgemeinen haben alle Automaten ein solch vorgegebenes Schema. Automaten setzen sich zusammen aus Zuständen und Übergängen. Ein festgelegtes Schema gibt vor, wann ein Automat von einem Zustand in einen anderen übergeht.

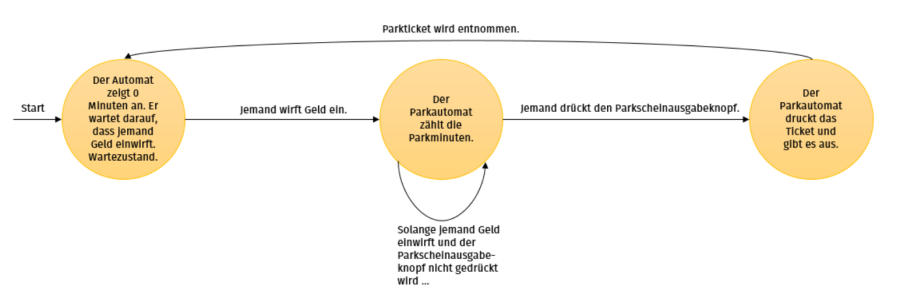
Noch einmal zurück zu dem Parkscheinautomaten, vor dem Laura und Manfred stehen:

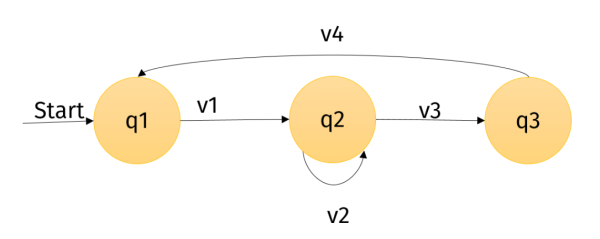
Beschriftet man die Zustände und Übergänge ein wenig anders, sieht das Ganze so aus:

Dieser Automat hat die folgenden Zustände:

• q1. Der Automat wartet auf eine Eingabe. → Wartezustand.
• q2. Der Automat merkt sich, wie viel Geld eingeschmissen wurde.
• q3. Der Automat druckt das Parkticket und gibt es aus.

Ausserdem hat der Automat die folgenden Übergänge:

• v1. Geld wird eingeschmissen. → Der Automat wechselt von q1 zu q2.
• v2. Es wird mehr Geld eingeworfen. → Der Automat bleibt in q2 und zählt die Minuten.
• v3. Der Knopf „Parkschein ausgeben“ wird gedrückt. → Der Automat wechselt in q3.
• v4. Das Parkticket wird entnommen. → Der Automat wechselt zurück in q1.

Diese Abstraktion (Verallgemeinerung) hat den Vorteil, dass nun eine gewisse Vergleichbarkeit mit anderen Automaten geschaffen wird und so generelle Aussagen und allgemeine Betrachtungen möglich sind.

Eine einfache Supermarktkasse funktioniert folgendermaßen:

• Wird ein Preis eingegeben, addiert die Kasse diesen zum Gesamtpreis.
• Drückt jemand die Taste „Kassieren“, wird der Gesamtpreis angezeigt und die Geldlade geöffnet.
• Wird die Geldlade geschlossen, wartet die Kasse darauf, dass erneut ein Preis eingegeben wird.

Ordne die verschiedenen Zustände der Kasse und die Aktionen des Kassierers/der Kassiererin den Zuständen und Übergängen der Skizze zu.

Vergleiche die Kasse mit dem Parkautomaten.

Dir ist vielleicht schon aufgefallen, dass viele Automaten am "ersten" Zustand einen Pfeil mit der Beschriftung "Start" haben. Dieser Zustand wird auch Startzustand genannt. Komplementär zum Startzustand gibt noch einen weiteren "besonderen" Zustand: den Endzustand. Dieser wird im Allgemeinen durch einen doppelten Kreis gekennzeichnet. Ein Automat kann auch mehrere Endzustände haben. Auf die besondere Bedeutung von Endzuständen gehen wir später näher ein.

Benenne die Start- und Endzustände der folgenden zwei Automaten:

Die Supermarktkasse von oben hat die folgenden Zustände und Übergänge.

Die Kasse hat die folgenden Zustände:

• q1. Wartezustand; die Kasse wartet auf die Eingabe eines Preises.
• q2. Ein Preis wurde eingegeben, der Knopf „Kassieren“ wurde allerdings noch nicht gedrückt.
• q3. Der Gesamtpreis wird angezeigt, und die Geldlade ist geöffnet.

Die Skizze hat die folgenden Übergänge:

• v1. Der erste Preis eines Artikels wird eingegeben.
• v2. Ein weiterer Preis wird eingegeben.
• v3. Der Knopf „Kassieren“ wird gedrückt.
• v4. Die Geldlade wird geschlossen.

Welchen Zustand könnte man hier als Endzustand wählen?

Wie eingangs beschrieben, reagiert ein Automat auf Aktionen. So wechselt der Parkscheinautomat zum Beispiel beim Einwurf von 5Cent den Zustand. Eine Folge von Aktionen wird Eingabe genannt.

So sind die Aktionen:

 5 ct einwerfen – 10 ct einwerfen – 5 ct einwerfen – Knopf drücken – Parkschein entnehmen

eine Eingabe.

Ein Automat verarbeitet eine Eingabe, indem er die einzelnen Aktionen der Reihe nach betrachtet und entsprechend reagiert.

Reagieren heißt hier: Der Automat sucht einen Übergang, der vom aktuellen Zustand ausgeht und mit der Aktion, die an der Reihe ist, beschriftet ist.

Eingaben können unterschiedlich aussehen; es können sowohl Folgen von Zahlen, Wörtern, Zeichen oder Buchstaben sein. Bei realen Automaten sind dies Knöpfe, Münzen, Auswahltasten etc.

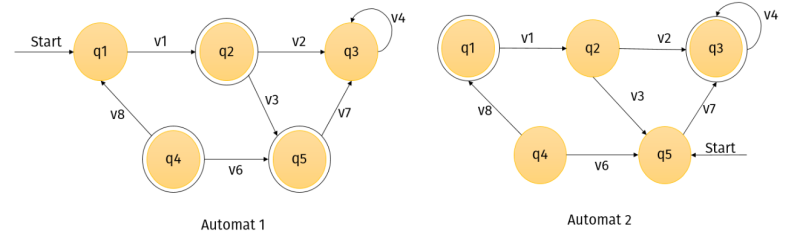
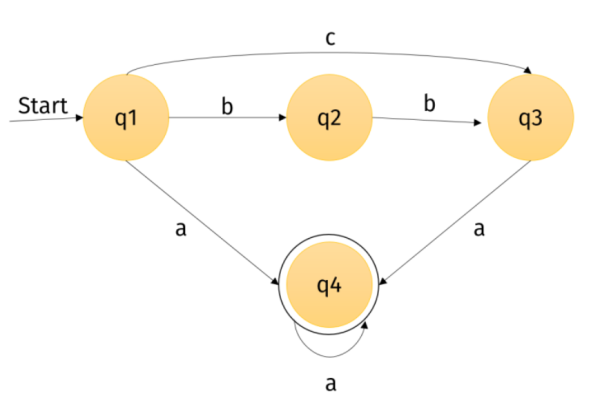
Um Automaten strukturiert und übersichtlich darstellen zu können, werden oft Kürzel an den Übergängen verwendet. Diese Standardisierung (Vereinheitlichung) ermöglicht außerdem die Analyse der Eigenschaften von Automaten. Im folgenden Beispiel werden die Übergänge durch Buchstaben abgekürzt: Der folgende Automat hat die Zustände: q1, q2, q3, q4. Der Zustand q1 ist der Startzustand, q4 der Endzustand.

Außerdem hat dieser Automat sechs Übergänge, die mit den Buchstaben a, b und c markiert sind.

Wie reagiert der Automat auf die Eingabe caa?

• Start bei q1.
• Wechsel mit c von q1 zu q3.
• Wechsel mit a von q3 zu q4.
• Der Automat bleibt im Zustand q4 mit a.

Nach der Eingabe caa befindet sich der Automat also in dem Zustand q4.

Die Eingabe bbb hingegen kann der Automat nicht verarbeiten, da es vom Zustand q3 aus keinen Übergang gibt, der mit b beschriftet ist!

Wie reagiert der Automat oben auf die folgenden Eingaben?

bbaaa
aa
aab
caaaa

Wie bereits erwähnt, können Eingaben sehr unterschiedlich sein. Deswegen ist es nötig, zu jedem Automaten anzugeben, aus welchen Zeichen (z. B. Buchstaben) die Sprache besteht, die er versteht. Die Menge dieser Zeichen wird Eingabealphabet genannt. So ist das Eingabealphabet des Automaten aus dem Beispiel oben {a, b, c}. Das Eingabealphabet muss natürlich nicht aus Buchstaben bestehen, es kann sich auch aus ganzen Wörtern, Sätzen oder Zahlen, Knopfdrücken oder Touchscreengesten zusammensetzen.

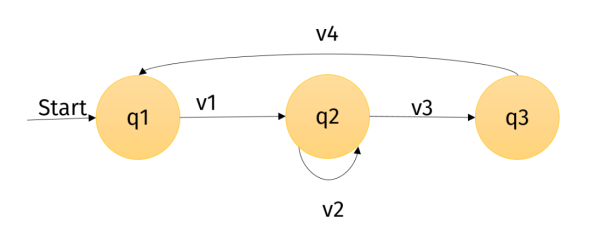
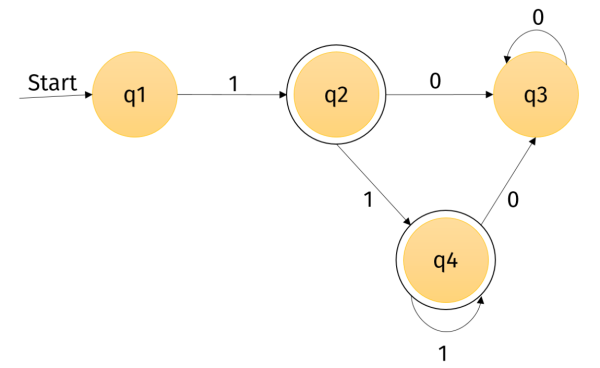
Nenne den Startzustand, den Endzustand und das Eingabealphabet dieses Automaten.

Beschreibe außerdem, wie der Automat sich auf die Eingaben 1111, 1100 bzw. 1001 verhält.

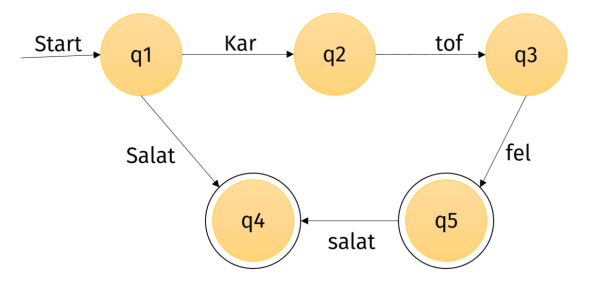
Nenne auch den Startzustand, die Endzustände und das Eingabealphabet dieses Automaten. Beschreibe außerdem das Verhalten des Automaten auf die folgenden drei Eingaben:

Kartoffelsalat
Salat
Nudelsalat

In dieser Zusatzaufgabe schreibst du am Computer ein Programm, das einen Automaten simuliert. Das Programm soll ausgeben, in welchem Zustand sich der Automat nach Bearbeitung einer bestimmten Eingabe befindet.

Betrachte erneut den folgenden Automaten:

Das Eingabealphabet ist die Menge {0, 1}.

Du sollst nun ein Javaprogramm schreiben, das diesen Automaten simuliert.

Lege dir dazu ein Integer-Array an, in dem die Eingabe gespeichert wird. Die Eingabe kannst du in dem Programm vorgeben, z. B. durch int[] eingabe = {1, 0, 0, 1};

Dein Programm soll nun ausgeben, in welchem Zustand sich der Automat befindet, nachdem er die Eingabe vollständig abgearbeitet hat.

Bestimme die Start- und Endzustände des folgenden Automaten

Fülle folgenden Lückentext aus:

Ein Automat setzt sich aus ____________ und _______________ zusammen. Es gibt un-
terschiedliche Arten von Zuständen. Einer der „besonderen“ Zustände wird mit einem
Pfeil gekennzeichnet; diesen Zustand nennt man _________________________. Ein
weiterer „besonderer“ Zustand wird dagegen mit einem doppelten Kreis gekennzeich-
net; hierbei handelt es sich um den _______________________________.
Ein festgelegtes Schema gibt vor, wann ein Automat von einem _______________ in
einen anderen ________________ übergeht. Allgemein sagt man, dass der Automat
eine _______________ aus dem _____________________ verarbeitet.

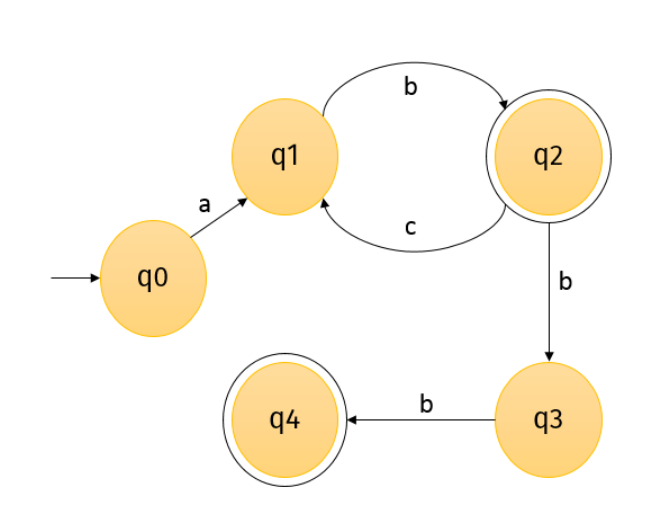
Betrachte noch einmal den Automaten der Lernfortschrittskontrolle (L1) oben.

In welchem Zustand befindet sich der Automat nach Bearbeitung der folgenden Eingaben?

1. abcbb
2. abcbcbbb

Setze die folgenden Zeichenketten so fort, dass sich der Automat nach Bearbeitung der Zeichenkette in einem Endzustand befindet. Wähle dabei immer die kürzeste Möglichkeit.

1. a
2. abc
3. abb