Eisverkäufer: Dominierende Menge

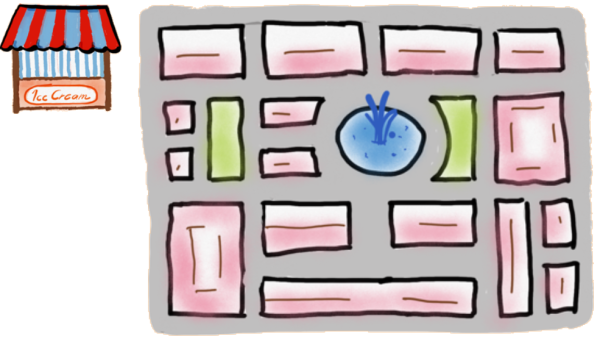
In einem heißen Sommer möchte ein Eisproduzent in einer Stadt eine perfekte Versorgung der Bevölkerung mit Eis sicherstellen (natürlich, um möglichst viel zu verdienen) und stellt dazu Eisstände auf. Kein Bürger und keine Bürgerin der Stadt soll zu weit laufen müssen. Daher muss an jeder Straßenecke entweder ein Eisstand stehen oder - wenn es keinen Eisstand gibt - an mindestens einer der benachbarten Straßenkreuzungen ein Eisstand zu finden sein.

(A1)

Finde für die oben abgebildete Stadt geeignete Standorte für die Eisstände, so dass möglichst wenige Eisstände benötigt werden, da das der Firma Kosten spart. Anmerkung: Auch die Straße um alle Häuser außen herum zählt als Straße und damit die äußeren Ecken als Kreuzungen.

Hier kannst du die Eisstände direkt im Browser platzieren

Fachbegriff: Dominierende Menge

Gegeben ist ein Graph G
Gesucht ist eine Teilmenge der Knoten - die dominierende Menge - , so dass jeder Knoten, der nicht in der dominierenden Menge ist, mindestens einen Nachbarknoten aus der dominierenden Menge hat.

Zu diesem Problem gibt es zwei Fragestellungen:

Existenz: Gibt es überhaupt eine dominierende Menge mit weniger Knoten, als der Graph hat?
Optimale Lösung: Finde eine dominierende Menge mit möglichst wenigen Knoten.

Kein effizienter Algorithmus?

Du hast sicher eine Lösung für den Eisverkäufer gefunden, die die Abdeckung der Stadt mit Eisständen sicherstellt. Aber ist das die beste Lösung? Vielleicht geht es ja mit weniger Eisständen.

Es ist kein cleverer Algorithmus bekannt, der gezielt die richtigen Knoten auswählt. Man müsste daher alle möglichen Teilmengen der Knoten daraufhin testen, ob sie eine überdeckende Menge darstellen, und unter den überdeckenden Mengen die mit der geringsten Anzahl an Knoten auswählen.

(A2)

Berechne, wie viele mögliche Teilmengen der Knoten es beim Einstiegsbeispiel gibt. Beachte, dass jeder Knoten zur Teilmenge dazugehören kann oder auch nicht. Wie ändert sich die Anzahl der Möglichkeiten, wenn ein Knoten hinzukommt?

Lösung

(A3)

Führe im Simulationsmodus des Programms Graphentester den Algorithmus "Dominierende Menge (Vollständig)" bei den Graphen graph_knotenX.csv (X=5-10) aus und bestimme den Zeitbedarf. Stelle dabei die Geschwindigkeit so ein, dass beim Graphen mit 5 Knoten ca. 3 Sek. benötigt werden. Hinweis: Die Klasse ist zu finden bei algorithmen/GraphAlgo_DominatingSetBacktracking.

Untersuche, wie sich der Zeitbedarf durch einen zusätzlichen Knoten verändert.

(A4)

Stelle auf maximale Geschwindigkeit um und führe den Algorithmus beim Graph mit 10 Knoten erneut aus.
Sage den Zeitbedarf für den Graphen mit 15 Knoten vorher. Überprüfe deine Vorhersage.
Berechne, wie lange es für das Einstiegsbeispiel dauern würde.

Würde man also alle Teilmengen (alle möglichen Lösungen) überprüfen und davon die tatsächlich beste wählen, so wäre die Laufzeit exponentiell ($O(2^n)$ mit n = Anzahl der Knoten). Das ist für Algorithmen eine geradezu katastrophale Laufzeit.
In so einem Fall versucht man fast immer eine andere algorithmische Vorgehensweise zu finden, die vielleicht nicht die perfekte Lösung findet, aber eine vergleichsweise gute Lösung in dafür viel kürzerer Zeit findet. Die alternative Lösung hat dann typischerweise eine polynomielle Laufzeit ($O(n^c)$ mit c = Konstante).

Näherungslösung

Wenn es zu lange dauert, die beste Lösung zu finden, ist man manchmal auch mit einer guten Lösung zufrieden: Ein oder zwei Eisstände mehr als bei der optimalen Lösung sind in einer Stadt kein Problem.

(A5)

Beschreibe, wie du vorgegangen bist, um deine Lösung im Einstiegsbeispiel zu finden.

Greedy-Strategie

Die Greedy-Strategie (gieriger Algorithmus) ist ein Ansatz, um Näherungslösungen zu bestimmen. Sie zeichnen sich dadurch aus, dass sie nacheinander die Möglichkeit auswählen, die zum Zeitpunkt der Wahl den größten Gewinn bzw. das beste Ergebnis verspricht.

Beim Problem der dominierenden Menge fügt man schrittweise der gesuchten Teilmenge Knoten hinzu, bis sie eine überdeckende Teilmenge darstellt. In jedem Schritt versucht man natürlich, den Eisstand möglichst gut zu platzieren. Hat man einen Knoten jedoch einmal hinzugefügt, nimmt man diese Entscheidung nicht mehr zurück, auch wenn man später erkennt, dass die Entscheidung nicht optimal war.

Es stellt sich jetzt allerdings die Frage, was genau eine "möglichst gute" Platzierung in einem Schritt bedeuten soll.

(A6)

Analysiere, welcher Knoten als nächstes hinzugefügt werden sollte.

Notiere zunächst deine Überlegungen und kontrolliere die Ergebnisse dann mit dem Graphentester "Dominierende Menge (Greedy (a-i))" anhand der Graphen graph_knoten10 und graph_knoten15. ¹⁾ Beim Graphen mit 10 Knoten enthält die optimale Lösung der dominierenden Menge 2 Knoten, beim Graphen mit 15 Knoten 4 Knoten. Du kannst also untersuchen, wie gut eine Strategie funktioniert. Notiere dir am besten pro Graph und Strategie die jeweilige Lösung, um dann die insgesamt beste Lösung ermitteln zu können.

a) der Knoten mit den meisten Nachbarknoten.
b) der Knoten mit den wenigsten Nachbarknoten.
c) der Knoten, der die meisten Knoten neu überdeckt.
d) der Knoten der die wenigsten Knoten neu überdeckt.
e) ein Knoten, der von einem schon ausgewählten Knoten die Entfernung 3 hat.
f) ein noch nicht überdeckter Knoten mit Entfernung 2 von einem schon ausgewählten Knoten.
g) ein noch nicht überdeckter Knoten mit Entfernung 3 von einem schon ausgewählten Knoten.
h) der noch nicht überdeckte Knoten, der von möglichst vielen schon ausgewählten Knoten die Entfernung 3 hat.
i) der noch nicht überdeckte Knoten mit der größten Entfernung von allen schon ausgewählten Knoten.

(A7)

Wende die erfolgversprechenden Strategien auf das Einstiegsbeispiel an.

(A8)

Begründe, warum die Näherungslösungen viel schneller als die optimale Lösung gefunden werden.

¹⁾

Ursprünglich waren hier die Graphen "graph_domknotenXX" vorgesehen, diese scheinen aber nicht zu funktionieren. Dort sind die dominierenden Knoten einer optimalen Lösung mit einem Stern (*) markiert.