Hat ein gegebener Graph einen Eulerkreis?

Um entscheiden zu können, ob ein gegebener Graph einen Eulerkreis besitzt oder nicht, müssen wir zwei Kriterien überprüfen:

Alle Knotengrade müssen gerade sein
Der Graph muss zusammenhängen

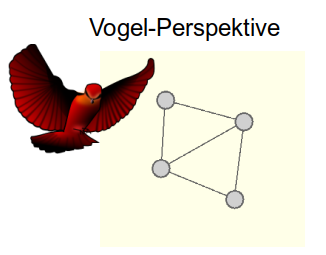
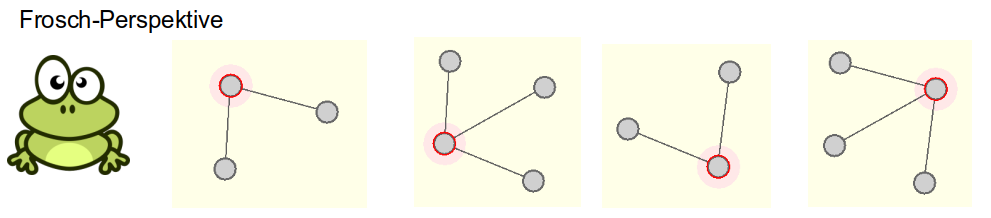
Die Froschperspektive

Bei Algorithmen, die auf Graphen operieren, müssen wir einen Perspektivwechsel vornehmen: Wir sehen einen Graphen aus der "Vogelperspektive", d.h. wir nehmen den gesamten Graphen mit all seinen Knoten und Kanten wahr und lassen dann nur unsere Augen wandern - wenn uns eine Information fehlt, schauen wir einfach an die entscheidende Stelle und das Problem ist gelöst.

Wenn wir einen Graphen algorithmisch verarbeiten wollen, müssen wir schrittweise durch die Knotenanordnung wandern - wir sehen niemals weiter als bis zum Ende der nächsten Kante. Wir müssen also die Frosch-Perspektive einnehmen.

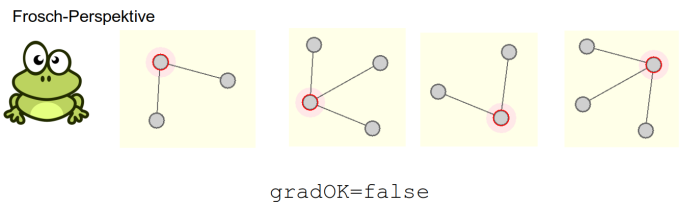
Überprüfung des Knoten-Grades

Setze gradOK auf true
Für jeden Knoten k:
   Wenn Grad(k) ungerade, setze gradOK auf false

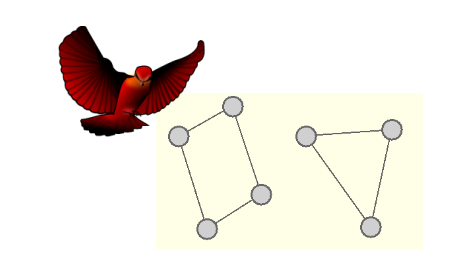
Überprüfung des Zusammenhangs

Aus der Vogelperspektive ist das sofort klar - dieser Graph hängt nicht zusammen:

Der Frosch ist allerdings etwas ratlos:

(A1)

Finde eine algorithmische Vorgehensweise, wie der Frosch herausfinden kann, ob der Graph zusammenhängend ist. Um dieses Ziel zu erreichen, hat der Frosch die folgenden Werkzeuge und Fähigkeiten zur Verfügung:

Der Frosch kann…

Knoten / Kanten markieren
Bei Knoten eine Zahl eintragen
Knoten einfärben
Alle Knoten der Reihe nach durchgehen
Einen beliebigen Knoten als Startknoten wählen
Zum Nachbarknoten springen
Eine ToDo-Liste noch zu bearbeitender Knoten anlegen

Lade dir den Graphentester herunter und versuche im Experimentiermodus einen Algorithmus zu finden, der herausfindet, ob ein gegebener Graph zusammenhängend ist oder nicht.

Notiere den Algorithmus als Text oder in Pseudocode.

Hilfestellung 1

Hilfestellung 2

Pseudocode des Algorithmus, um den Zusammenhang zu testen

Der hier beschriebene Algorithmus bestimmt die Anzahl der vom Startknoten aus erreichbaren Knoten und vergleicht sie mit der Gesamtzahl der Knoten.

Zusammenhang des Graphen:
Markiere den Startknoten als besucht
Erzeuge eine leere ToDo-Liste und füge den Startknoten hinzu
Setze nr auf 0

Wiederhole solange die ToDo-Liste nicht leer ist
  Erhöhe nr um 1
  Nimm den ersten Knoten aus der ToDo-Liste heraus
  Markiere ihn und gib ihm die Nummer nr

  Wiederhole für jeden seiner Nachbarn
    Falls der Nachbarknoten noch nicht besucht ist
      Kennzeichne ihn als "besucht"
      Füge ihn am Ende der ToDo-Liste hinzu
    Ende-Falls
  Ende-Wiederhole
Ende-Wiederhole

Falls nr = Anzahl der Knoten im Graph
  Der Graph ist zusammenhängend
Sonst
  Es gibt mehrere Zusammenhangskomponenten
Ende-Falls

Variante: Statt am Ende der ToDo-Liste können die Nachbarn auch am Anfang der ToDo-Liste eingefügt werden.

Dateien

Filename	Filesize	Last modified
auswahl_379.png	21.8 KiB	09.11.2022 20:53
auswahl_380.png	35.0 KiB	09.11.2022 20:54
auswahl_381.png	57.6 KiB	09.11.2022 20:57
auswahl_383.png	21.5 KiB	09.11.2022 21:00
auswahl_384.png	35.9 KiB	09.11.2022 21:01
graphentester.odp	226.2 KiB	09.11.2022 21:12
graphentester.pdf	165.1 KiB	09.11.2022 21:12