Kartenfärben

Landkarten werden normalerweise koloriert, um einzelne Gebiete gut unterscheiden zu können. Dabei dürfen benachbarte Gebiete nicht in derselben Farbe gefärbt werden. Es sollen dabei möglichst wenige Farben verwendet werden.

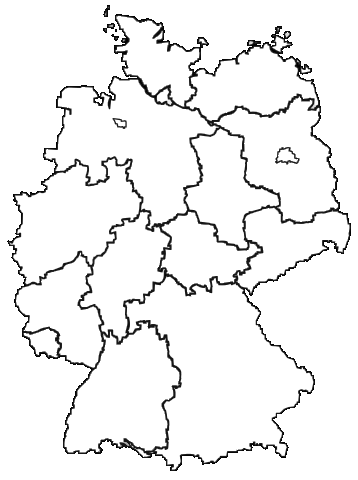
Färbe die Karte der Bundesländer nach der beschriebenen Regel.
Auf dieser Internetseite lässt sich die Deutschlandkarte auch online einfärben.

¹⁾

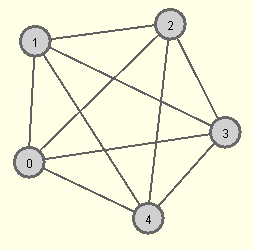
Die Ausgangssituation soll nun als Graph modelliert werden. Dabei stehen die Knoten für die Gebiete der Landkarte, zwei Knoten haben eine gemeinsame Kante, wenn Sie auf der Karte eine gemeinsame Grenzlinie haben.

Varianten:

• Verwende dabei möglichst wenige Farben.
• Ist es möglich, den Graphen mit k Farben zu färben?

Der hier beschriebene Algorithmus findet nicht die perfekte Lösung, d.h. die minimale Anzahl an Farben, aber eine gute Näherungslösung. Er arbeitet dabei nach dem Greedy-Verfahren, er wählt für ein Land die momentan am besten erscheinende Lösung.

Zunächst wird eine Reihenfolge festgelegt, in der die Farben verwendet werden sollen.

z.B. Rot - Blau - Grün - Gelb - Lila - Orange - Braun (es müssen ausreichend viele Farben sein) Dann betrachtet man der Reihe nach alle Knoten. Für jeden Knoten wird dann Folgendes gemacht: Man schaut jeden der Nachbarknoten an und merkt sich, dass seine Farbe schon verwendet wurde. Dann wählt man aus der Liste der Farben die erste noch nicht benutzte Farbe aus und färbt den Knoten in dieser Farbe.

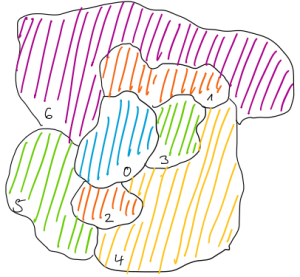
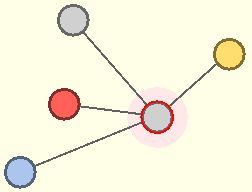
z.B. Der rot umrandete Knoten ist aktuell an der Reihe. Alle Nachbarknoten werden betrachtet und ihre Farben ermittelt.

Die erste noch nicht benutzte Farbe ist grün. Daher wird der Knoten grün gefärbt.

Teste das eben beschriebene Greedy-Verfahren an den Karten dieser Internetseite.

Begründe die obigen Aussagen.

Lösung

Beschreibe eine Situation (Landkarte incl. Reihenfolge der Länder), in der der Greedy-Algorithmus mehr als 4 Farben erfordert.

Lösungsvorschlag

Landkarten lassen sich immer mit vier Farben einfärben⁴⁾. Bestimme die Anzahl der möglichen Färbungen (ohne Beachtung der Regel, dass Nachbarländer nicht die gleiche Farbe haben dürfen) einer Landkarte aus 20 Ländern mit 4 Farben.

Lösung

Für das Kartenfärbeproblem ist kein Algorithmus bekannt, der eine optimale Lösung bestimmt, ohne dabei alle Möglichkeiten auszuprobieren. Begründe die Notwendigkeit eines Näherungsalgorithmus.

Lösung

Erläutere, durch welche besondere Eigenschaft ein Graph, der eine Landkarte repräsentiert, die Beschränkung auf 4 Farben ermöglicht.

Lösung

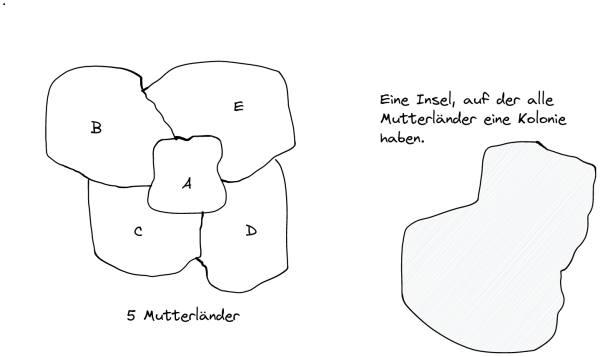
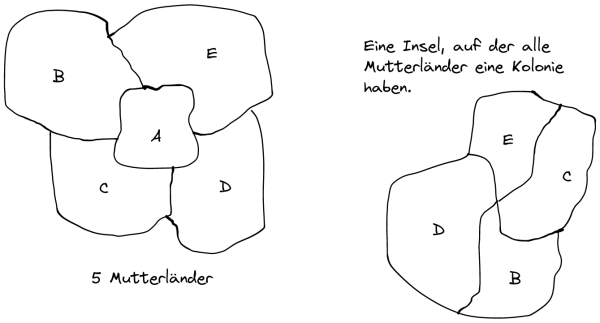
(A) Eine Variante des Kartefärberoblems ist das Kolonialproblem: Einige Länder haben Kolonien, die nicht direkt mit dem Mutterland verbunden sind. Dabei sollen das Mutterland und seine Kolonien in der gleichen Farbe eingefärbt werden. Weiterhin soll gelten, dass benachbarte Länder bzw. Kolonien nicht in der gleichen Farbe eingefärbt werden dürfen. Es ist nicht bekannt, ob es eine Obergrenze der Anzahl der benötigten Farben gibt.

Tipp:

Lösung

(B) Modellierung

• Überführe die Karte in den dazugehörigen Graphen. Erläutere, wie Du die Forderung modellierst, dass das Mutterland und seine Kolonien in der gleichen Farbe gefärbt werden sollen.
• Begründe anhand des Graphen, warum die Obergrenze von vier Farben für eine Landkarte nicht mehr gilt.

Tipp

Lösung

Notiere den beschriebenen Algorithmus als Pseudocode und implementiere ihn selbst im Graphentester. Hinweise und Lösungsvorschläge findest du unten.

Pseudocode

Kartenfärbung:
Wiederhole für jeden Knoten k des Graphen
  
  Wiederhole für jede Farbe der Farbliste
     Setze die Farbe auf "unbenutzt"
  Ende-Wiederhole
  
  Wiederhole für jeden Nachbarknoten n von k
     Betrachte die Farbe des Knoten n
     Setze diese Farbe auf "benutzt"
  Ende-Wiederhole
  
  Wiederhole für jede Farbe der Farbliste
     Falls die Farbe "unbenutzt" ist
       Färbe den Knoten k mit dieser Farbe
       Brich die Schleife ab
     Ende-Falls
  Ende-Wiederhole

Ende-Wiederhole

Beispielimplementation

List<Knoten> knoten = g.getAlleKnoten();
for (Knoten aktuellerKnoten: knoten) {
  boolean[] farbenliste = new boolean[g.getAnzahlKnoten()+1];
  for (int i=0; i < farbenliste.length; i++){
    farbenliste[i]=false;
  }
 
  List<Knoten> nachbarn = g.getNachbarknoten(aktuellerKnoten);
  for (Knoten k : nachbarn){
    farbenliste[k.getFarbe()]=true;
  }
 
  for (int i=1; i<farbenliste.length; i++){
    if (!farbenliste[i]) {
      aktuellerKnoten.setFarbe(i);
      break;
    }
  }
}