Inhaltsverzeichnis
Texterzeugung mit Herrn Markow
Ein Markow-Prozess - benannt nach dem russischen Mathematiker Andrei Andrejewitsch Markow - ist ein mathematisches Modell, das verwendet wird, um die zukünftige Entwicklung eines Systems vorherzusagen. Es basiert auf der Idee, dass die zukünftige Entwicklung des Systems nur von seinem aktuellen Zustand abhängt und nicht von seiner gesamten Vergangenheit.
Nonsense-Texterzeugung
Wir können einen Markow-Prozess verwenden, um vorherzusagen, welche Buchstaben(folge) als nächstes ausgegeben werden soll, basierend auf dem aktuellen Buchstaben(folge) im Text.
Einen solchen Markow-Prozess kann man sich sehr gut als Graph veranschaulichen:
Man beginnt bei einem beliebigen Buchstaben, die Pfeile des gerichteten Graphen geben die erlaubten Übergänge an. So kann man Worte bilden, die gewissen Regeln unterliegen - die erlaubten nächsten Buchstaben hängen davon ab, was der gerade aktuelle Buchstabe ist.
- HAU
- LAU
- LAUB
- RAUB
- RAUS
- HAUS
- AUA
- UAUB
Sind "erlaubte" Worte, die so erzeugt werden können.
Die tatsächlich gewählten Übergange sind dabei zufällig, die so erzeugten Worte unterliegen also den Regeln welche der Graph vorgibt, es ist aber gleich wahrscheinlich, ob nach einem U ein B, ein S oder ein A angefügt wird.
Ausprobieren
Das BlueJ-Projekt "Markow-Texter" erlaubt es, einen solchen Textgenerator auszuprobieren und zu untersuchen.
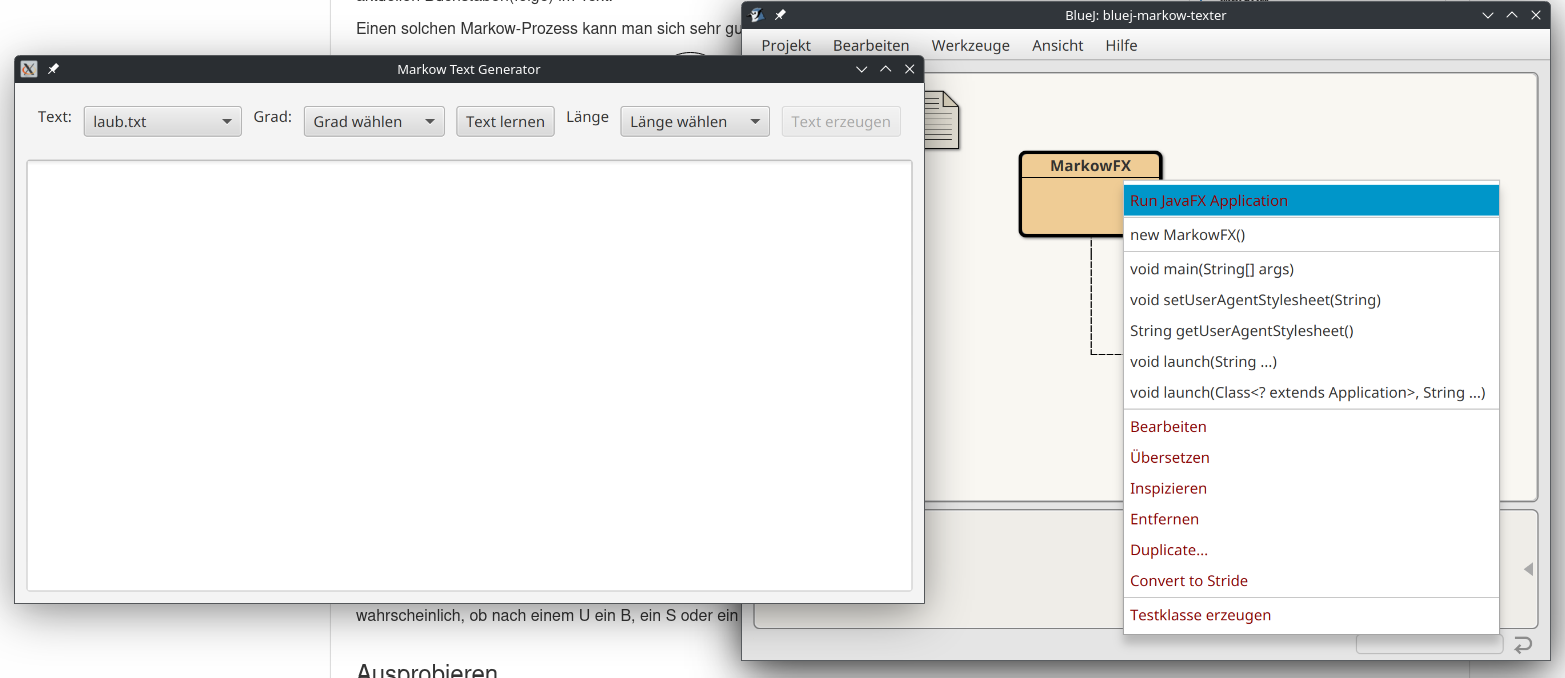
Lade das Bluej-Projekt herunter2). Um das Programm zu verwenden, öffnet man das BlueJ-Projekt und führt die JavaFX Anwendung aus, indem man mit der rechten Maustaste auf die Klasse "MarkowFX" klickt und im Menü den Punkt "Run JavaFX Application" auswählt - dann sollte sich das Programmfenster öffnen:

(A1)
Teste das Programm mit der "Trainingsdatei" laub.txt.
Wichtig: Beim einlesen des Trainingstextes werden alle Zeichen in Kleinbuchstaben konvertiert, paarige Zeichen wie Anführungszeichen entfernt und Zeilenumbrüche durch ein großes "N" ersetzt.
- Wähle als Grad 1
- Klicke dann auf
Text lernen - Analysiere die Ausgabe im Textfeld. Notiere, was diese Bedeuten könnte.
- Wähle als Textlänge 40 Zeichen
- Klicke anschließend auf
Text erzeugen
Wie funktionierts?
Die Funktionalität des Markow Texters findet sich in der Klasse Markow3).
Die wichtigsten Bestandteile:

uebergaenge: Das ist eine HashMap, das den Übergangsgraphen speichert. Dort wird festgehalten, welche Folgezeichen zu einem aktuellen Zustand erlaubt sind.
private Map<String, Map<Character, Integer>> uebergaenge;
Beim Lernen des Texts wird hier z.B. folgendes eingetragen:
"a": u(6) N(2)
Das bedeutet, dass uebergaenge["a"] eine Liste von Zeichen mit ihrer zugehörigen Häufigkeit enthält, mit der sie im Anschluss an "a" aufgetreten sind: Das Zeichen "u" folgte 6 mal auf ein "a", ein Zeilenumbruch ("N") folgte 2 mal auf ein "a".

(A2)
Erhöhe den Grad auf 2 und lerne erneut den Text laub.txt. Interpretiere die Ausgabe des Lernprozesses. Der Text findet sich im Unterverzeichnis texte des Projekts. Öffne die Datei laub.txt mit einem Editor und überprüfe deine Ideen.
Teste weitere Grade beim Lernen des Textes.
 Die Methoden
Die Methoden lerneText(String textQuelle, int grad) und lerneUebergang(String letzteZeichen, char naechstesZeichen):
/** * Lerne Text */ public void lerneText(String text, int grad) { this.grad = grad; uebergaenge.clear(); for (int i = 0; i < text.length() - grad; i++) { // Hier wird das "Zustandsfenster" der Länge grad // über den Text "geschoben" String zustand = text.substring(i, i + grad); // Das ist das Zeichen, das auf den aktuellen Zustand folgt char naechstesZeichen = text.charAt(i + grad); // Lerne den gefundenen Übergang lerneUebergang(zustand, naechstesZeichen); } } /** * Hier wird ein gefundener Übergang überprüft und * passend in der HashMap eingetragen */ public void lerneUebergang(String zustand, char naechstesZeichen) { // Versuche die Übergangs-Map für den aktuellen Zustand zu lesen Map<Character, Integer> folgeZeichenMap = uebergaenge.get(zustand); // Wenn es für den Zustand noch keine Einträge gibt... if(folgeZeichenMap == null) { // Zuerst eine neue Map für die Folgezeichen anlegen. Die ist erst mal leer... uebergaenge.put(zustand, new HashMap<>()); } // Jetzt gibt es für den Zustand auf alle Fälle ein Map mit den Folgezeichen // Nun muss man entscheiden, ob das aktuelle Folgezeichen neu da rein muss // oder ob nur seine Anzahl erhöht werden muss. folgeZeichenMap = uebergaenge.get(zustand); Integer anzahl = folgeZeichenMap.get(naechstesZeichen); if(anzahl == null || anzahl == 0) { folgeZeichenMap.put(naechstesZeichen, 1); } else { folgeZeichenMap.put(naechstesZeichen, anzahl + 1); } uebergaenge.put(zustand, folgeZeichenMap); }

(A3)
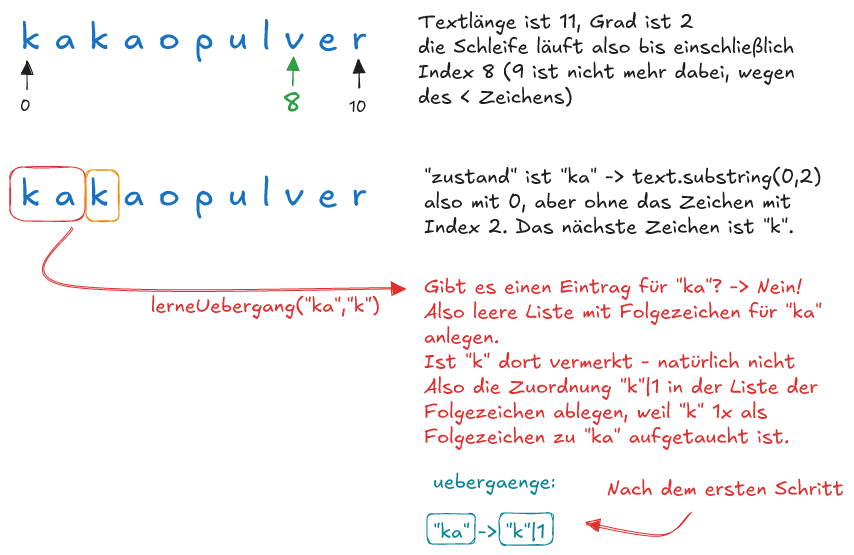
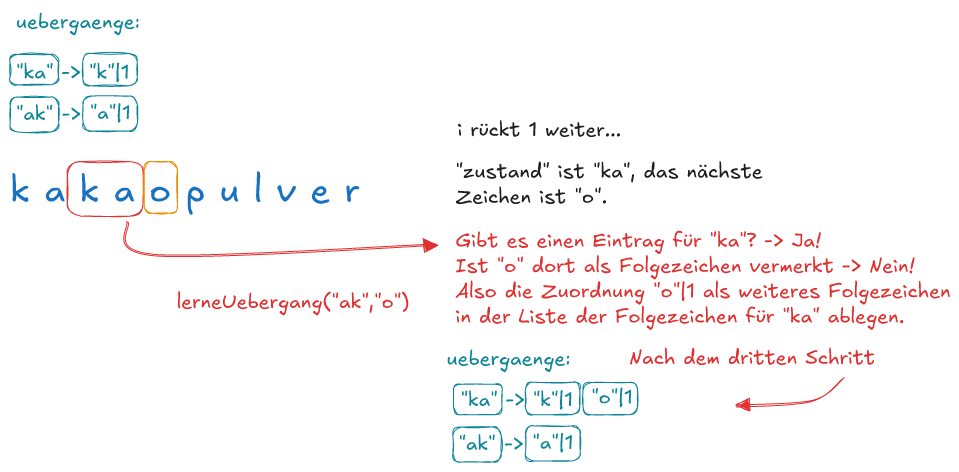
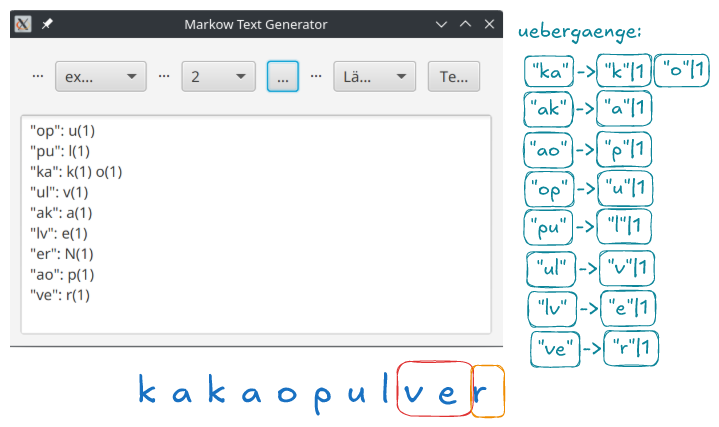
Vollziehe am Wort kakaopulver mit dem Grad 2 nach, was die beiden Methoden machen. Welche Übergänge sind am Ende des Lernprozesses in der HashMap uebergaenge abgelegt?
Du kannst das mit dem Markow-Texter überprüfen, indem du den Text kakaopulver in die Datei experiment.txt einträgst und das Programm lernen lässt.
 Die Methoden
Die Methoden erzeugeText(String anfang, int laenge) und zufaelligerUebergang(String aktuellerZustand):
/** * Erzeuge Text */ public String erzeugeText(String anfang, int laenge) { String aktuellerZustand = anfang; StringBuilder resultat = new StringBuilder(anfang); for (int i = 0; i < laenge; i++) { char naechstesZeichen = zufaelligerUebergang(aktuellerZustand); aktuellerZustand = aktuellerZustand.substring(1) + naechstesZeichen; resultat.append(naechstesZeichen); } return resultat.toString().replaceAll("N","\n"); } /** * Wählt ein zufälliges Folgezeichen. Die Häufigkeit der Zeichen wird * nicht berücksichtigt. */ char zufaelligerUebergang(String aktuellerZustand) { Map<Character, Integer> folgeZeichen = uebergaenge.get(aktuellerZustand); if(folgeZeichen != null) { // Zufalsgenerator initialisieren Random generator = new Random(); // Die Keys der HashMap in ein Array umwandeln. Diese Methode // funktioniert nur, wenn alleZeichen eine Array vom Typ // Object ist. Object[] alleZeichen = folgeZeichen.keySet().toArray(); // mit generator.nextInt(alleZeichen.length) wird eine Zufallszahl erzeugt // die über den Index ein zufälliges Element auswählt. // Bevor das Element zurückgegen werden kann, muss es nach char // gecastet werden. return (char) alleZeichen[generator.nextInt(alleZeichen.length)]; } else { return ' '; } }

(A4)
Vollziehe nach wie das Erzeugen von Texten abläuft.
- Erstelle eine Methode
public char gewichteterUebergang(String aktuellerZustand), der bei der Auswahl des nächsten Zeichens die Häufigkeiten der Zeichen berücksichtigt - Für Fortgeschrittene: Dupliziere den Markow-Texter in ein neues BlueJ-Projekt und passe dieses so an, dass er Wörter lernt anstatt Zeichen, so dass das jeweils nächste Wort anhand der vorhergehenden Worte bestimmt wird.