Grundlagen der Aussagenlogik

Eine Aussage bezeichnet ein sprachliches Gebilde, dem in sinnvoller Weise genau eine der beiden Eigenschaften wahr oder falsch zugeordnet werden kann. Man kürzt ab: wahr=1, falsch=0.

In der Aussagenlogik oder Schaltalgebra verwenden wir

Variablen, die meist mit $x_0,x_1,x_2...$ bezeichnet werden. Bei diesen Variablen handelt es sich um boolsche Werte, sie können also nur zwei Zuständen (0 - Falsch, 1 - Wahr) annehmen.
Logische Funktionen ordnen einer oder mehreren boolschen Variablen einen Funktionswert zu, sie werden oft mit $y$ bezeichnet. Der Funktionswert kann ebenfalls nur 1 (wahr) oder 0 (falsch) sein. Logische Funktionen lassen sich sehr gut als Wahrheits- oder Wertetabellen darstellen, da durch die beschränkte, diskrete Anzahl der Variablenkombinationen häufig eine Auflistung aller Funktionswerte möglich ist.
"Gerechnet" wird mit den logischen Verknüpfungen
- AND: ∧
- OR: ∨
- NOT: ¬
Beim Rechnen gelten - ähnlich wie die Punkt vor Strich Regeln: "Klammer vor NOT vor AND vor OR"

Die Verknüpfung mit UND ∧ nennt man Konjunktion
Die Verknüpfung mit ODER ∨ nennt man Disjunktion

"Rechenregeln" der Schaltalgebra

Kommutativgesetz (Vertauschung erlaubt)

$x_0 \land x_1 = x_1 \land x_0$
$x_0 \lor x_1 = x_1 \lor x_0$

Distributivgesetz (Gießkannenregel)

$x_0 \land (x_1\lor x_2)= (x_0 \land x_1) \lor (x_0 \land x_2$)
$x_0 \lor (x_1\land x_2)= (x_0 \lor x_1) \land (x_0 \lor x_2$)

Neutralelement

$x_0 \lor 0 = x_0$
$x_0 \land 1 = x_0$

Komplement

$x_0 \land \lnot x_0 =0$
$x_0 \lor \lnot x_0 = 1$

Assoziativgesetze (Klammern dürfen bei gleichen Operatoren weggelassen/umgesetzt werden)

$(x_0 \land x_1) \land x_2 = x_0 \land x_1 \land x_2 = x_0 \land (x_1 \land x_2)$
$(x_0 \lor x_1) \lor x_2 = x_0 \lor x_1 \lor x_2 = x_0 \lor (x_1 \lor x_2)$

Idempotenzgesetze

$x_0 \land x_0 = x_0$
$x_0 \lor x_0 = x_0$

Absorptionsgesetze

$x_0 \lor (x_0\land x_1) = x_0$
$x_0 \land (x_0\lor x_1) = x_0$

De Morgan’sche Regel ("ausmultiplizieren des NICHT")

$\lnot(x_0 \lor x_1)= \lnot x_0 \land \lnot x_1$
$\lnot(x_0 \land x_1)= \lnot x_0 \lor \lnot x_1$

Beispiel

Gegeben ist die logische Funktion $f$ durch

$$f=(\lnot x_0 \land \lnot x_1 \land x_2) \lor (\lnot x_0 \land x_1 \land \lnot x_2) \lor (\lnot x_0 \land x_1 \land x_2) \lor ( x_0 \land \lnot x_1 \land x_2)$$

(A1)

Wieviele Zeilen hat die Wahrheitstabelle dieser Funktion?
Schreibe die Wahrheitstabelle der Funktion auf¹⁾.

Lösung

Nun stellt sich die Frage, ob man den doch sehr langen Funktionsterm vielleicht unter Verwendung der Rechengesetze so vereinfachen kann, dass man einen kürzeren Term als Ergebnis erhält, der dieselbe Wahrheitstabelle hat, also dieselbe logische Funktion beschreibt.

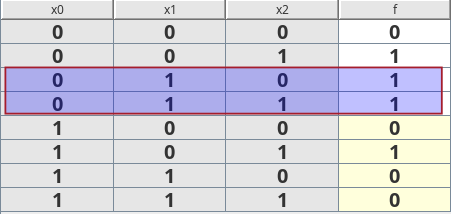
Wenn man die Wertetabelle der Beispielfunktion betrachtet, fällt auf:

(1) Wenn $x_0=0$ und $x_1=1$ ist der Funktionswert 1, gleichgültig, was für einen Wert $x_2$ annimmt.

Das entspricht den beiden eingerahmten Termen:

Rechnerisch kann man hier den Teilterm $(\lnot x_0 \land x_1)$ ausklammern, so dass der eingerahmte Term zu $$(\lnot x_0 \land x_1) \land (\lnot x_2 \lor x_2)$$

wird.

(A2)

Vereinfache die folgenden logischen Terme:

$f = x_1\land(\lnot x_2) \lor x_1\land x_2$
$g = x_1\land (\lnot x_2)\land x_3 \lor x_1\land(\lnot x_2)\land(\lnot x_3) \lor (\lnot x_1)\land (\lnot x_2)\land (\lnot x_3) $
$h = (\lnot x_1)\land (\lnot x_2)\land(\lnot x_3) \lor (\lnot x_1)\land(\lnot x_2)\land x_3 \lor (\lnot x_1)\land x_2\land x_3 \lor x_1\land (\lnot x_2)\land (\lnot x_3) \lor x_1\land x_2 \land x_3 \lor x_1 \land x_2\land ( \lnot x_3) $

¹⁾

Das geht auch mit einem Tabellenverarbeitungsprogramm….