Dies ist eine alte Version des Dokuments!
Der Dijkstra Algorithmus
Häufig möchte man kürzeste Pfade in gewichteten Graphen bestimmen. Die Länge des Pfads entspricht in diesem Fall nicht einfch der Zahl der Kanten, sondern der Summe der Kantengewichte entlang des Pfads.
Ein wichtiges Beispiel für diese Situation sind Navigationssysteme. Die Kantengewichte hängen von der genauen Problemstellung ab: Wenn man die kürzeste Strecke zwischen zwei Knoten im Graphen sucht, trägt man an den Kanten den Abstand zwischen benachbarten Knoten ein, sucht man den schnellsten Weg, repräsentieren die Kantengewichte die Fahrzeiten.
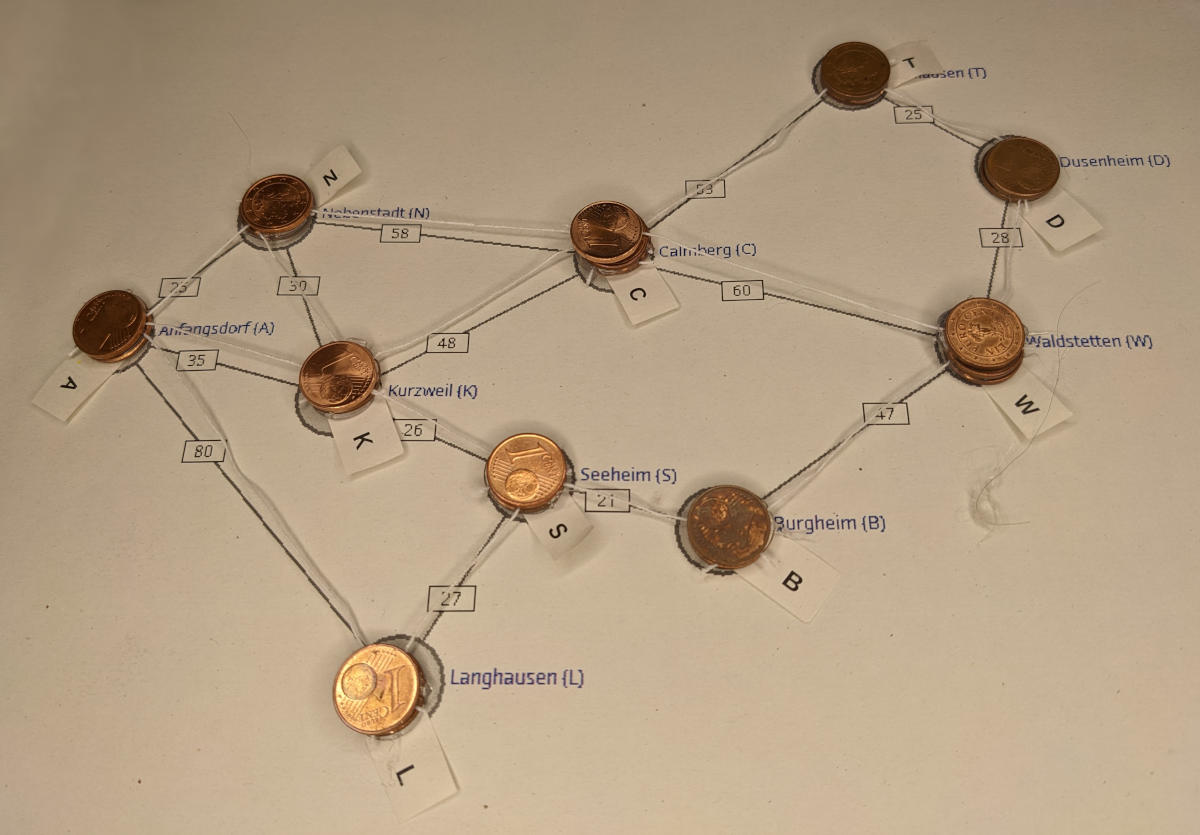
In diesem Sinne können die Zahlen an den Kanten im folgenden Beispielgraphen Entfernungen oder Zeiten repräsentieren.
Die Länge des direkten Pfads von Anfangsdorf nach Langhausen ist 80, die Länge des Pfads von Anfangsdorf nach Langhausen über Kurzweil und Seeheim ist 88. der direkte Pfad ist also kürzer.
Die Idee des Dijkstra Algorithmus
Gegeben ist:
- Ein gewichteter Graph G(V,E).1)
- Ein Startknoten S
- Ein Zielknoten Z
Gesucht: Der kürzeste Weg durch den Graphen, der von S nach Z führt.
Eine andere Formulierung des Problems ist, dass zu einem gegebenen Graphen mit Startknoten S die Pfadlänge von S zu allen anderen Knoten im Graphen gefunden werden soll.
Lösungsansatz mit Pfiff
Der folgende Lösungsansatz führt direkt zum 1959 von Edsger Wybe Dijkstra gefundenen Algorithmus zur Lösung dieses Problems.
Dazu stellt man sich zunächst vor, die Knoten seien durch Fäden miteinander verbunden.
Nun fasst man das so entstandene Netz am Startpunkt und hebt diesen an und zieht ihn langsam nach oben. Auf diese Weise heben sich nacheinander alle Knoten des Graphen von der Unterlage ab, und zwar in der Reihenfolge der Entfernung vom Startknoten: Der Knoten mit dem geringsten Abstand zuerst, dann der zweitnächste und so weiter.
Um den kürzesten Weg zu einem gegebenen Zielknoten Z zu finden, geht man also folgendermaßen vor: Man hebt den Startknoten an und zieht ihn nach oben. Knoten für Knoten löst sich von der Tischplatte. Man stoppt, wenn sich der Zielknoten beginnt, sich abzuheben. Wenn man nun die straff gespannten Fäden zurückverfolgt, führen diese eindeutig zum Startpunkt - und dieser Weg von S zu Z ist der kürzeste Weg zwischen den Knoten.

(A1)
- Schaue dir den Film an, der den Vorgang zeigt und stelle anhand der Bewegung der Centstücke die Reihenfolge der Knotenentfernungen im Beispielgraphen auf. Überprüfe die so gefundene Reihenfolge anhand der Kantengewichte.
- Erläutere kurz, warum man so tatsächlich den kürzesten Weg zwischen Start- und Zielknoten findet.
Der Computer zieht die Fäden
Möchte man dieses Trickreiche Vorgehen in einem Algorithmus implementieren, muss man anstelle der Fäden andere Kriterien finden. Der Schlüssel zum Ersatz der Fäden ist die Antwort auf folgende Frage:
Welcher Knoten ist stets der nächste, der von der Unterlage abgehoben wird?