Dies ist eine alte Version des Dokuments!
Levelorder Traversierung, Iterative Tiefensuche
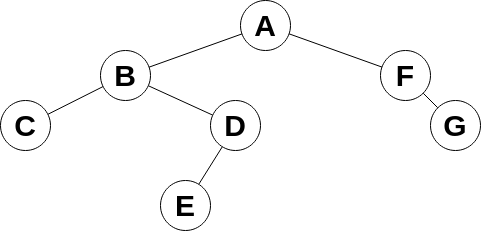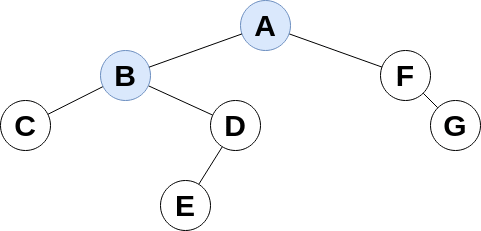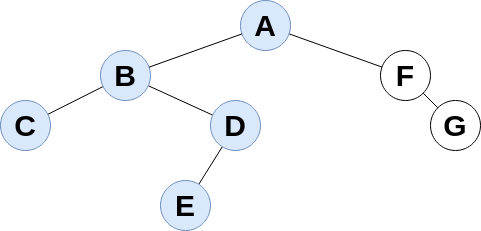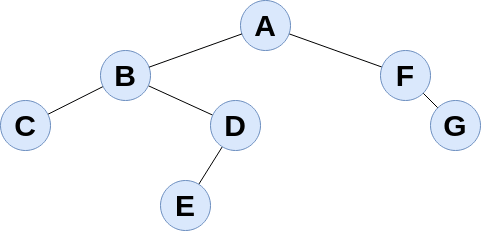
Bei den drei rekursiv implementierbaren Traversierungen wird der Baum zuerst in die Tiefe durchwandert bis hin zu seinen Blättern ("Tiefensuche") - hier noch einmal am Beispiel bei der Preorder-Traversierung:
Bei der Levelorder Traversierung werden auf jedem Niveau des Baums erst alle Knoten besucht, bevor auf das nächste Niveau gewechselt wird, in unserem Beispielbaum ergibt sich damit die Traversierungsreihenfolge: A→B→F→C→D→G→E. Der Algorithmus zur Levelorder Traversierung ist nicht rekursiv.
Iterative Traversierung
Die rekursiven Implementationen der Traversierungen versagen ihren Dienst, wenn die Bäume zu tief werden, da der Call-Stack für die Rekursion nicht beliebig wachsen kann. Bei Java ist seine Größe auf ca. 256kB beschränkt, wenn diese Größe überschritten wird, erhältst du einen Stack Overflow Error:
Die einfachste Lösung für dieses Problem ist es, den Stack, in dem man darüber Buch führt, welche Knoten des Baums als nächstes zu bearbeiten sind, selbst zu verwalten:
Von der Rekursion zur Iteration
Die folgende Tabelle stellt den rekursiven Pseudocode zur Ermittlung der Knotenzahl einer iterativen Variante gegenüber.
| Rekursiv | Iterativ |
|---|---|
anzahl(b: Binaerbaum):
falls b == null:
return 0
sonst:
t1 = anzahl(b.links)
t2 = anzahl(b.rechts)
return 1 + t1 + t2
| anzahl(b: Binaerbaum):
todo = new Stack
todo.push(b)
zaehler = 0
solange todo nicht leer:
tmp = todo.pop()
zaehler++
falls tmp.rechts != null:
todo.push(tmp.rechts)
falls tmp.links != null:
todo.push(tmp.links)
return zaehler
|
Während die rekursive Variante die Verwaltung der noch zu bearbeitenden Knoten dem Aufrufstack der Rekursion überlässt, implementiert die iterative Variante einen eigenen "todo"-Stack mit, dem die den in den nächsten Schritten zu verarbeitenden Knoten verwaltet werden.
Suche im Baum

(A1) Tiefensuche
Arbeite mit der folgenden Bluej-Vorlage: https://codeberg.org/qg-info-unterricht/binaerbaum-iterativ
Du kannst in der Klasse "Testbaeume" anpassen, welche baumdefinitionen geladen werden sollen: Entweder 100 "große" Bäume oder 5 "kleine" Bäume.
- Implementiere zunächst den Stack, so dass du anschkließen die Knoten des Baums verwalten kannst. Schlage wenn nötig auf den entsprechenden Wiki-Seiten nach.
- Implementiere dann die eine Iterative-Traversierung des Baums. Gelingt es dir, Pre-, In- und Postorder Traversierung zu implementieren? Mit den "kleinen" Bäumen kannst du die Traversierungen gut nachvollziehen.
- Erweitere deine Traversierung zu einer Tiefensuche, die
- einen Knoten eines bestimmten Wertes findet
- den ersten Knoten findet, dessen Wert zwischen den an die Suchmethode zu übergebenden Parametern
lowundhighliegt.

(A2) Breitensuche
* Implementiere zunächst den nötigen Queue, so dass du anschließend die Knoten des Baums verwalten kannst. Schlage wenn nötig auf den entsprechenden Wiki-Seiten nach.
- Implementiere dann die eine Iterative-Traversierung des Baums. Gelingt es dir, Pre-, In- und Postorder Traversierung zu implementieren? Mit den "kleinen" Bäumen kannst du die Traversierungen gut nachvollziehen.
- Erweitere deine Traversierung zu einer Tiefensuche, die
- einen Knoten eines bestimmten Wertes findet
- den ersten Knoten findet, dessen Wert zwischen den an die Suchmethode zu übergebenden Parametern
lowundhighliegt.
Material
| Filename | Filesize | Last modified |
|---|---|---|
| baeume_traversierung_iterativ.odp | 106.8 KiB | 14.02.2022 14:21 |
| baeume_traversierung_iterativ.pdf | 170.4 KiB | 14.02.2022 14:21 |
| levelorder.gif | 44.1 KiB | 14.02.2022 19:37 |
| stackoverflow.png | 13.9 KiB | 14.02.2022 14:24 |