Die Set-Implementationen im Detail

Die einfachste Lösung ist, wenn der ADT Set als interne Datenstruktur eine ArrayList verwendet. Beim Einfügen muss immer getestet werden, ob der Wert bereits in der ArrayList vorkommt. Dazu muss unter Umständen jedes Element der ArrayList untersucht werden.

• Einfache Implementation
• Speicherbedarf relativ gering (etwa proportional zur Anzahl der Werte)

• Suche nach einem Element bei großen Mengen aufwendig (proportional zur Anzahl der Werte)

Man kann eine Menge von Integer-Zahlen auch in eine einzelne Integer-Zahl verpackt darstellen, indem man die entsprechenden Bits in ihrer Binärdarstellung setzt. Man spricht dann von einem Bitvektor.

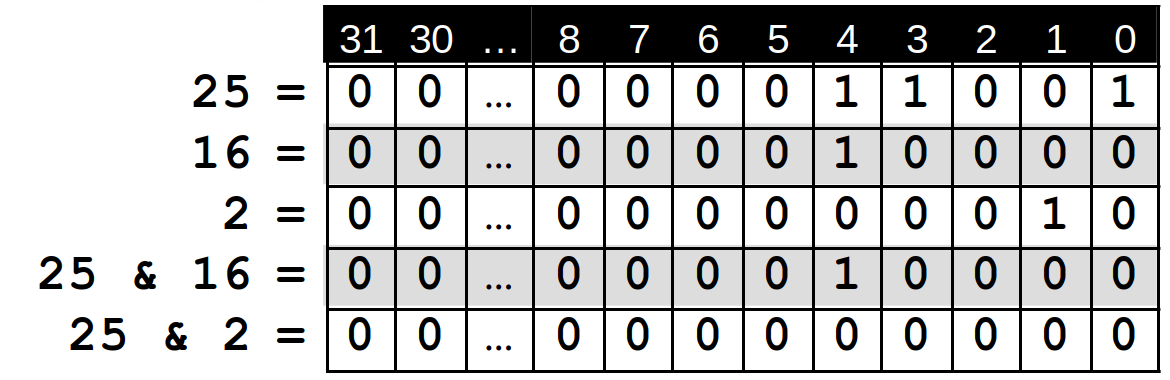
Beispiel: Die Menge {0,3,4} soll gespeichert werden. Dazu setzt man die Bits an den Stellen 0,3 und 4 auf 1 und alle anderen auf 0 und bestimmt anschließend die Dezimaldarstellung der Binärzahl. Das Resultat ist die Zahl 25:

Da eine Integer-Zahl in Java 32 Bit lang ist, kann man mit einer Integer-Zahl also für die Zahlen von 0 bis 31 darstellen, ob sie in einer Menge enthalten sind oder nicht.

Um herauszufinden, ob eine Zahl enthalten ist, kann man mit dem binären UND-Operator prüfen, ob das entsprechende Bit gesetzt ist:

int vier_gesetzt = 25 & 16;  // Ergebnis: 16
int eins_gesetzt = 25 & 2;   // Ergebnis: 0

Der binäre UND-Operator verknüpft zwei int-Zahlen (nach Umwandlung in die Binärdarstellung) und setzt im Ergebnis ein Bit auf 1, wenn die entsprechenden Bits in beiden Operanden auf 1 gesetzt sind.

Eine Zahl ist in der Menge enthalten, wenn bei der UND-Verknüpfung ein Wert herauskommt, der nicht 0 ist.

Um einen Wert zu einem Bitvektor hinzufügen, verwendet man die binäre ODER-Verknüpfung.

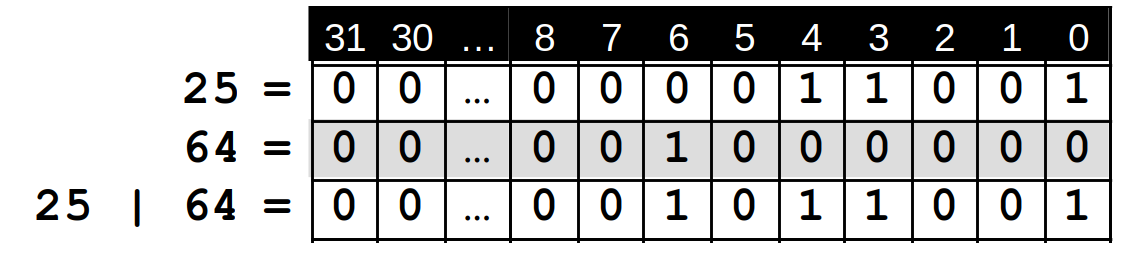
Beispiel: Zur Menge {0,3,4} soll die 6 hinzugefügt werden. Man setzt also den Bitvektor auf

 bitvektor = bitvektor | 64; // neuer Wert 89

Der binäre ODER-Operator verknüpft zwei int-Zahlen und setzt im Ergebnis ein Bit auf 1, wenn mindestens eines der entsprechenden Bits in den beiden Operanden auf 1 gesetzt ist.

Beim Setzen eines Bits muss nicht geprüft werden, ob es bereits gesetzt ist – der ODER-Operator verändert in diesem Fall den Bitvektor nicht.

Zum lesen und setzen von Elementen benötigt man die entsprechenden Zahlen, letztlich in Binärdarstellung. Diese Zahlen, die man zum Auslesen oder Setzen von Bits verwendet werden als Bitmaske bezeichnet.

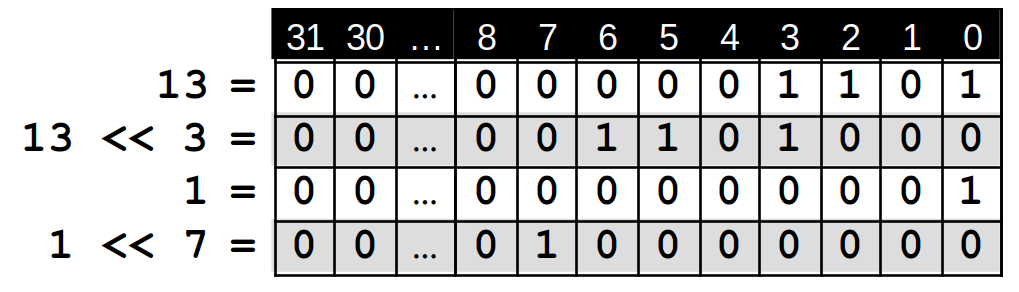
Eine Maske, bei der als niederwertigstes Bit nur das n-te Bit von rechts gesetzt ist, entspricht der Zahl 2ⁿ. Schnell und effizient erhält man diese Zahl, indem man die Zahl 1 um n Stellen nach links „verschiebt“.

In Java wird eine solche Bitverschiebung ("bit shift") nach links mit dem Operator « erreicht:

int y = 1 << 7;  // y ist  1*27 = 128

Man kann auch andere Zahlen als die 1 verschieben:

int x = 13 << 3; // x ist 13*23 = 104

Mit einer einzelnen 32-Bit-Zahl kann man Mengen der Zahlen 0 bis 31 abbilden. Will man größere Werte erlauben, benötigt man eine ArrayList von Integer-Zahlen.

Die k-te Zahl der ArrayList repräsentiert damit die Elemente mit den Werten 32·k bis 32·k+31.

Das Element n wird also durch das Bit n%32 in der Zahl daten[n/32] repräsentiert.

Beim Einfügen muss die ArrayList ggf. um Elemente erweitert werden, so dass sie groß genug ist.

Pseudocode:

einfuegen(n: int)
  k = n / 32
  solange Länge von daten ≤ k:
    hänge 0 an daten an
  bit = n % 32
  maske = 1 << bit
  daten[bit] = daten[bit] | maske

• Sehr speichereffizient, wenn die Werte nicht zu groß sind
• Lesender Zugriff in konstanter Anzahl von Schritten möglich
• Schreibender Zugriff meistens schnell möglich

• Wenn nur wenige, aber große Werte gespeichert werden, wird Speicher verschwendet
• Konzept ist nur zum Speichern von Integer-Zahlen anwendbar

Die Hashtable verwendet ein Array, das die Werte der Menge enthält.

Das Problem ist, dass die Suche nach einem Wert unter Umständen sehr lange dauert – insbesondere, wenn es gar nicht in der Menge vorhanden ist.

Die Idee des Hashings ist, dass man einem Wert "ansieht", wo er im Array stehen muss. Wir nehmen als erstes Beispiel ein Array mit 10 Plätzen:

Um den Speicherort eines Wertes x zu bestimmen, berechnet man h(x) = x mod arraylaenge und legt ihn dort ab:

einfuegen(42) → Position 42 mod 10 = 2, daten[2] = 42
einfuegen(77) → Position 77 mod 10 = 7, daten[7] = 77