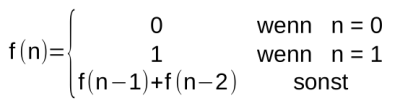Dies ist eine alte Version des Dokuments!
Übungen 3: Aufrufbäume

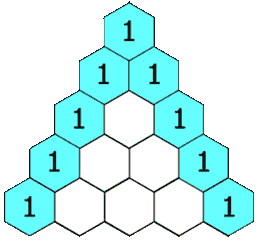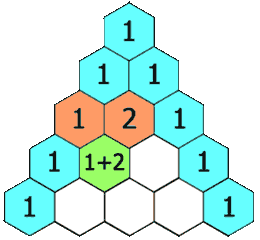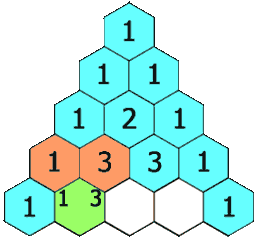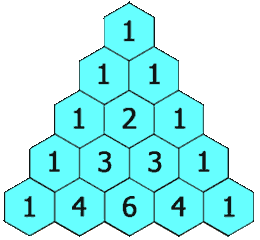
(A1) Pascalsches Dreieck
Beim Pascalschen Dreieck werden die jeweils oberhalb liegenden Felder addiert und ergeben das darunter liegende Feld, wie in der Animation rechts zu sehen ist.
Man kann eine rekursive Funktion implementieren, die den Wert des Feldes in Zeile z und Spalte s des Pascalschen Dreiecks berechnet: pascal(int z, int s): int.

(A2) Ficonacci mit Baum
Die Fibonacci-Funktion (auch als Fibonacci-Folge bezeichnet) ist definiert als:
Die ersten Werte der Fibonacci-Funktion sind 0, 1, 1, 2, 3, 5, 8, 13, … Die Definition kann einfach in eine rekursive Methode übersetzt werden:
fib(n: int): int
wenn n ≤ 1:
gib n zurück
sonst:
gib fib(n-1) + fib(n-2) zurück
(A) Gib die vier Werte der Fibonacci-Folge an, die auf das Folgenglied 13 folgen.
(B) Stelle die ausgeführten Methodenaufrufe bei der Ausführung von fib(4) als
Baum dar.
(C) Begründe, warum die Anzahl der Methodenaufrufe für fib(n) weniger als 2n+1> beträgt.
(D) Implementiere eine Methode fibIterativ(n: int): int, die dasselbe Ergebnis wie fib berechnet, die aber ohne Rekursion arbeitet.