Dies ist eine alte Version des Dokuments!
Eisverkäufer
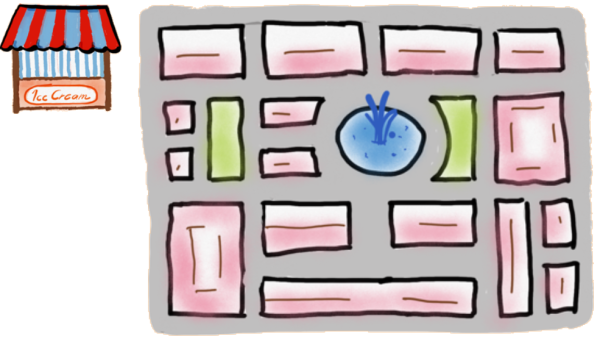
In einem heißen Sommer möchte ein Eisproduzent in einer Stadt eine perfekte Versorgung der Bevölkerung mit Eis sicherstellen (natürlich, um möglichst viel zu verdienen) und stellt dazu Eisstände auf. Kein Bürger und keine Bürgerin der Stadt soll zu weit laufen müssen. Daher muss an jeder Straßenecke entweder ein Eisstand stehen oder - wenn es keinen Eisstand gibt - an mindestens einer der benachbarten Straßenkreuzungen ein Eisstand zu finden sein.

(A1)
Finde für die oben abgebildete Stadt geeignete Standorte für die Eisstände, so dass möglichst wenige Eisstände benötigt werden, da das der Firma Kosten spart. Anmerkung: Auch die Straße um alle Häuser außen herum zählt als Straße und damit die äußeren Ecken als Kreuzungen.
Fachbegriff: Dominierende Menge
- Gegeben ist ein Graph
G - Gesucht ist eine Teilmenge der Knoten - die dominierende Menge - , so dass jeder Knoten, der nicht in der dominierenden Menge ist, mindestens einen Nachbarknoten aus der dominierenden Menge hat.
Zu diesem Problem gibt es zwei Fragestellungen:
- Existenz: Gibt es eine dominierende Menge mit weniger als Knoten, als der Graph hat?
- Optimale Lösung: Finde eine dominierende Menge mit möglichst wenigen Knoten.
Keine gute Methode?
Du hast sicher eine Lösung für den Eisverkäufer gefunden, die die Abdeckung der Stadt mit Eisständen sicherstellt. Aber ist das die beste Lösung? Vielleicht geht es ja mit weniger Eisständen.
Es ist kein cleverer Algorithmus bekannt, der gezielt die richtigen Knoten auswählt. Man müsste daher alle möglichen Teilmengen der Knoten daraufhin testen, ob sie eine überdeckende Menge darstellen, und unter den überdeckenden Mengen die mit der geringsten Anzahl an Knoten auswählen.

(A2)
Berechne, wie viele mögliche Teilmengen der Knoten es beim Einstiegsbeispiel gibt. Beachte, dass jeder Knoten zur Teilmenge dazugehören kann oder auch nicht. Wie ändert sich die Anzahl der Möglichkeiten, wenn ein Knoten hinzukommt?

(A3)
Führe im Simulationsmodus des Programms Graphentester den Algorithmus "Dominierende Menge (Vollständig)" bei den Graphen "graph_knotenX.csv" (X=5-10) aus und bestimme den Zeitbedarf. Stelle dabei die Geschwindigkeit so ein, dass beim Graphen mit 5 Knoten ca. 3 Sek. benötigt werden. Untersuche, wie sich der Zeitbedarf durch einen zusätzlichen Knoten verändert.