Topologische Sortierung von Graphen

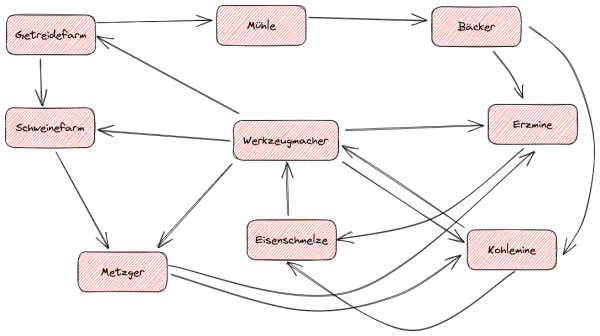
¹⁾ Bei einem Aufbausimulationsspiel kann man verschiedene Gebäude bauen. Jedes Gebäude produziert eine bestimmte Ware. Damit das Gebäude arbeiten kann, benötigt es seinerseits Waren anderer Gebäude als Rohstoff:

• Die Minen müssen mit Essen versorgt werden, das entweder Fleisch vom Metzger oder Brot vom Bäcker sein kann. Je nach Typ produzieren Minen Kohle oder Eisenerz.
• Die Eisenschmelze stellt daraus das vom Werkzeugmacher benötigte Eisen her.
• Der Werkzeugmacher heizt seine Schmiede mit Kohle und erzeugt aus dem Eisen Sensen für die Getreidefarm, Fleischermesser für den Metzger und Pickel für die Minen.
• Mit dem Getreide der Farm werden die Schweine gefüttert und in der Mühle das Mehl für den Bäcker gemahlen.
• Die Schweine werden vom Metzger geschlachtet.

Diese Abhängigkeiten machen es schwer zu entscheiden, in welcher Reihenfolge man die Gebäude bauen sollte, damit sie nicht ungenutzt herumstehen.

Gib (wenn möglich) eine sinnvolle Baureihenfolge der Gebäude an.

Modelliere die Situation im Aufbausimulationsspiel als gerichteter Graph.

• Was sind die Knoten, was die Kanten?
• Müssen die Kanten eine Richtung haben oder genügt es, Verbindungen herzustellen?
• Woran kannst du am Graphen erkennen, dass es für das Simulationsspiel keine topologische Sortierung gibt?

Lösung

Im Computerspiel gibt es zwei Möglichkeiten, Verklemmungen zu lösen.

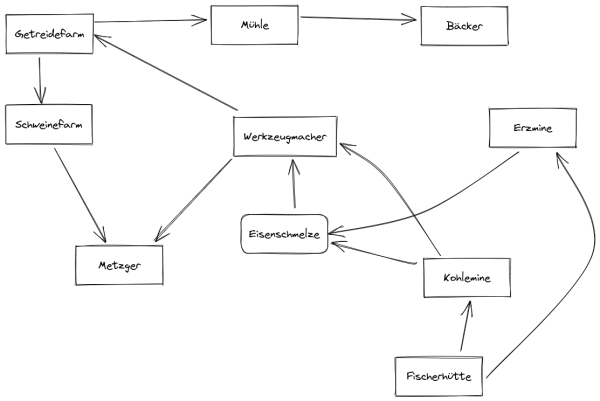
• Weitere Gebäude werden eingeführt: z.B. eine Fischerhütte, die ohne Voraussetzung Essen (Fisch) produziert.
• Man erhält eine Anzahl von Anfangsgegenständen, mit denen man die Produktion in Gang bringen kann: z.B. 20 Pickel.

Gib an, welche Kanten des ursprünglichen Graphen (zumindest vorübergehend) entfernt werden können, wenn man die Fischerhütte hinzufügt und zu Beginn 20 Pickel zur Verfügung stehen. Zeige, dass so die Verklemmung gelöst wird und eine topologische Sortierung nun möglich ist. Zeichne den zu dieser topologischen Sortierung gehörigen Graphen.

Lösung

Wichtig dabei ist, dass es innerhalb der Reihenfolge der Sortierung nicht notwendig ist, stets eine Kante von einem Knoten in der Sortierung zum nächsten zu haben. Es reicht, wenn man die Knoten von links nach rechts in einer Reihenfolge anordnen kann, so dass es keine Kanten gibt, die von rechts nach links zeigen. So kann man den Lösungsgraphen aus der vorigen Aufgabe durch Verschieben der Knoten folgendermaßen anordnen:

Das stellt eine gültige topologische Sortierung dar, auch wenn es keine Kante von der Kohle- zur Erzmine gibt. Man erkennt auf diese Weise auch sofort, dass es mehr als eine topologische Sortierung eines gerichteten Graphen geben kann, die Reihenfolge ist also nicht eindeutig:

Du kannst das selbst ausprobieren, indem du die folgende Datei aufbausimulation-graph-fischerhuette.zip herunterlädst und auspackst. Du erhältst die Datei Aufbausimulation-Graph-Fischerhuette.excalidraw. Diese kannst du in Excalidraw öffnen, nun kannst du die Knoten des Graphen auf einer Achse anordnen, so dass es keine Kanten gibt, die von rechts nach links zeigen.

Zum Vergleich, ikannst du versuchen, dasselbe Ergebnis mit dem ursprünglichen Graphen (ohne Fischerhütte) zu erzielen: aufbausimulation-graph.zip - man kann sehr gut erkennen, wie ein Zyklus im Graph eine topologische Sortierung unmöglich macht.

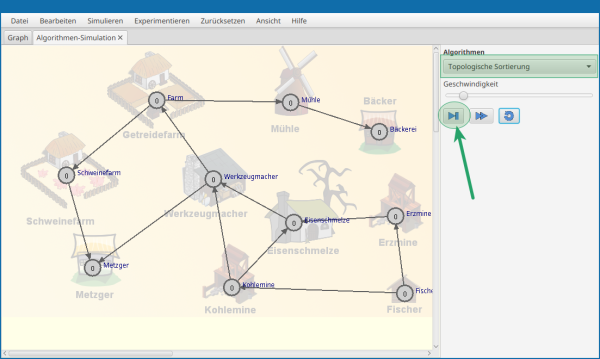
Öffne im Graphentester das Beispiel 02_topologischesortierung/02_aufbausimulation2.csv. Untersuche die Situation mit Hilfe des bereits im Graphentester implementierten Algrithmus "Topologogische Sortierung".

Formuliere den Algorithmus als Pseudocode.

Hilfestellung: Verbale Beschreibung des Algorithmus

Lösung: Pseudocode

Topologische Sortierung:
        
Für jeden Knoten k des Graphen: 
   setze den Wert des Knoten auf seinen Eingangsgrad

Setze topologische_Sortierung auf leer
        
Wiederhole solange es einen unmarkierten Knoten mit Wert 0 gibt
   Nimm einen unmarkierten Knoten k mit Wert 0
   Markiere k

   Füge k der topologische_Sortierung hinzu

   Für jeden Nachbarknoten n von k:
      reduziere den Wert des Knoten n um 1
Ende Wiederhole

Falls noch unmarkierte Knoten übrig sind:
  Ausgabe: es gibt keine topologische Sortierung
sonst:
  Ausgabe: topologische_Sortierung ist gefunden

Implementiere den Algorithmus selbst in einer eigenen Klasse unter "eigene Algorithmen". Teste deinen Algorithmus an den Beispielen 03_beispiel_obst.csv und 04_beispiel_obst2.csv.

+++ Lösungsvorschlag Algorithmus |

<code java> Reihenfolge String Reihenfolge = ""; Hole alle Knoten vom Graph g

      List<Knoten> alleKnoten = g.getAlleKnoten();
      // Schleife über alle Knoten
      for(Knoten k: alleKnoten) {
          int Eingangsgrad = g.getEingehendeKanten(k).size();
          k.setWert(Eingangsgrad);
          k.setFarbe(7);

      }
      step();
      boolean sort=true;
      while(alleKnoten.size() > 0 && sort) {
          Collections.sort(alleKnoten);
          Knoten k = alleKnoten.remove(0);
          if (k.getIntWert() == 0) {
              k.setFarbe(4);
              Reihenfolge += k.getInfotext() + " ";
              for(Knoten n: g.getNachbarknoten(k)) {
                  n.setWert(n.getIntWert()-1);
              }
          } else {
              sort=false;
          }
          step();
      }

      if (! sort) {
          System.out.println("Keine Sortierung möglich!");
      } else {
          System.out.println(Reihenfolge);
      }

</java>