Dies ist eine alte Version des Dokuments!
Das RSA Verfahren
Um die Funktionsweise des RSA Verfahrens nachzuvollziehen, musst du dir Klartext, Geheimtext und Schlüssel nicht als Bit-Folgen wie bei AES, sondern einfach als natürliche Zahlen vorstellen. Für den Computer macht das sowieso keinen Unterschied, da dieser alle Daten als Bit-Folge abspeichert udn verarbeitet.
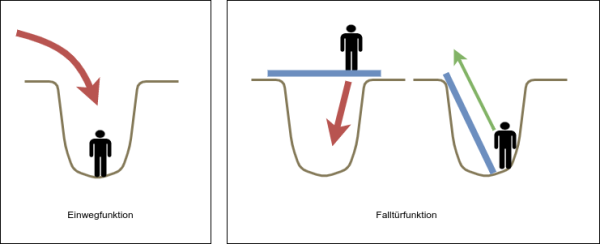
Einwegfunktionen und Falltürfunktionen
Im vorigen Wiki-Abschnitt haben wir uns mit der Modulo-Rechnung beschäftigt - diese ist in der Kryptografie wichtig, da einge der Modulo-Rechenarten sind sehr einfach durchgeführt werden können, ihre Umkehrung oft aber sehr ziemlich aufwändig ist.
So kann man die einfache Rechnung als Verschlüsselung und die komplizierte Umkehrung als Entschlüsselung verwenden – allerding nur dann, wenn es bei der komplizierten Umkehrung eine "versteckte Abkürzung" gibt, die man als Schlüssel nehmen kann.
Eine Funktion, die man einfach berechnen kann, bei der die Umkehrung aber nur mit großem Aufwand berechnet werden kann, nennt man Einwegfunktion.
Existiert eine "versteckte Abkürzung", also eine Zusatzinformation, mit der die ansonsten schwierige Umkehrung einfach gemacht wird, dann spricht man von einer Falltürfunktion.
Primzahl-Multiplikation als Einwegfunktion
Die (normale) Multiplikation zweier Primzahlen ist eine Einwegfunktion. Eine Primzahl-Multiplikation ist heutzutage mit Computerunterstützung einfach durchführbar, auch bei großen Zahlen macht das keine Probleme.
Im Gegensatz dazu sind keine effizienten Verfahren bekannt, mit denen aus dem Produkt zweier großer Primzahlen die beiden Faktoren bestimmt werden können.

(A1)
- Berechne im Kopf 13·17
- Bestimme die beiden Primzahlen, die miteinander multipliziert 1189 ergeben (auch im Kopf…)
Je größer die beiden Primzahlen sind, desto komplexer ist dieses sogenannte Faktorisierungsproblem: "Finde die beiden Primzahlen, die miteinander multipliziert die Zahl X ergeben". Bei Zahlen über tausend Bit Länge ist dieses Problem auch von aktuellen Superrechnern nicht mehr lösbar.
Die Multiplikation zweier großer Primzahlen ist eine Einwegfunktion. Es ist einfach, das Produkt zu berechnen, aber sehr schwierig/unlösbar, zu einer großen Zahl die beiden Prim-Faktoren zu bestimmen, die miteinander multipliziert diese Zahl ergeben.
Anmerkungen:
- Es lässt sich mathematisch nicht beweisen, dass dass die Primzahl-Multiplikation eine Einwegfunktion ist, es spricht jedoch alles dafür.
- Ein zentrales Problem dieser Einwegfunktion ist die Erzeugung großer Primzahlen. Das wird meist mit dem Miller-Rabin-Test gelöst, dessen Betrachtung hier aber zu weit führen würde.
Aus Einweg mach Falltür
Des RSA Verfahren basiert darauf, eine passende Falltürfunktion zu finden, die bei geeignet Wahl der beteiligten Zahlen eine Information als Schlüssel liefert, mit der sie umgekehrt werden kann.
Dazu benötigt man die Modulo-Rechnung aus einem der vorigen Wiki-Abschnitte:
- Die a-te Wurzel der Zahl b modulo n lässt sich leicht berechnen, wenn man φ(n) kennt und $a$ und $φ(n)$ teilerfremd sind. (Modulo-Wurzelziehen)
- φ(n) kann man leicht berechnen, wenn es sich bei n um das Produkt zweier Primzahlen p und q handelt. Dann gilt φ(n)=(p-1)·(q-1) (Modulo-Wurzelziehen)
Nach heutigem Kenntnisstand gibt es außer der im Abschnitt Modulo-Wurzelziehen beschriebenen Methode unter Zuhilfenahme von $φ(n)$ keine effektive Methode, die Modulo-Wuzel zu bestimmen. Damit ist das Modulo-Potenzieren eine Falltürfunktion - die Information, die sie umkehrbar macht sind die beiden Primzahlfaktoren aus denen der Modulus n berechnet werden kann. Da die Primzahlmultiplikation eine Einwegfunktion ist, kann man diese Faktoren nachträglich aus n bei genügend großen Primzahlen nicht mehr bestimmen.
Ablauf des RSA Verfahrens
Alice möchte, dass Bob ihr eine mit RSA verschlüsselte Mitteilung senden kann.
- Alice muss zunächst vorarbeiten: Sie wählt zufällig zwei große Primzahlen p und q und berechnet daraus den Modulus n=p·q.
- Anschließend wählt sie eine natürliche Zahl e, die teilerfremd zu φ(n) ist. Zur Erinnerung φ(n)=(p-1)·(q-1)). Die Zahlen n und e bilden zusammen den öffentlichen Schlüssel, den Alice öffentlich bekannt macht, also auch an Bon weitergibt. Ein Angreifer Mallory darf diesen auch erhalten.
Alice berechnet d:=e-1(mod φ(n)). d ist ihr geheimer Schlüssel, den sie natürlich für sich behalten muss.
Kennt Bob Alices öffentlichen Schlüssel e, dann verschlüsselt er damit seine Nachricht m, die er wie oben gezeigt als Zahl betrachtet. Dazu berechnet er c:=me (mod n). c ist der Geheimtext, den er an Alice schickt. Die Verschlüsselung entspricht einer Modulo-Exponentiation.
Die von Bob erhaltene Nachricht c kann Alice nun entschlüsseln, indem sie cd (mod n) berechnet. Das Ergebnis ist dann genau der Klartext m, den Bob abgeschickt hat. Dieses Entschlüsseln entspricht einem Modulo-Wurzelziehen: Alice zieht die e-te Modulo-Wurzel von c, indem sie die d-te Potenz berechnet. Mallory kann d nicht ermitteln, weil er die Faktorisierung von n nicht kennt.