Inhaltsverzeichnis
Routingprotokolle
In Netzwerktopologien, die nicht "schleifenfrei" sind, muss es Möglichkeiten geben, mit Hilfe derer Router bestimmen können, welches der beste Weg zu einem Zielrechner ist, dabei müssen selbstverständlich auch Wege über mehrere andere Router berücksichtigt werden.
Es existieren mehrere Protokolle, mit denen Router Informationen austauschen können, um ihrerseits ihre Routingkonfiguration zu optimieren - diese fallen grob in zwei Kategorien: Distanzvektor Routing-Protokolle und Link-State Routing-Protokolle.
Link-State Protokolle verwenden den Dijkstra-Algorithmus. Damit kann sich ein Router einen vollständigen Überblick über das ihn umgebende Netz verschaffen. Beispiele für Link-State Protokolle sind OSPF (Open Shortest Path First) oder IS-IS (Intermediate System to Intermediate System Protocol). Da uns der Dijkstra-Algorithmus später nochmal genauer beschäftigen wird, beschränken wir uns hier auf die Distanzvektor Protokolle.
Distanzvektor Routing-Protokolle basieren auf dem Bellman-Ford Algorithmus. Damit wird der "kürzeste" Weg ausgehend von einem Startknoten bestimmt, wobei die Verbindungen zwischen den Knoten verschiedene "Kosten" haben können. Der "kürzeste" oder "beste" Weg ist der, mit den geringsten Kosten.
Distanzvektor Routing-Protokolle geben in regelmäßigen Abständen (ca. alle 30 Sekunden und bei einer Änderung der Topologie) eine Kopie der eigenen Routing-Tabelle an ihren Nachbarn weiter. Auf diese Weise "wandern" Topologie-Änderungen durch das Netz.
Den Austausch der Routing-Tabellen kann man sich so vorstellen: Router A gibt seine Informationen zu Router B weiter. Router B gleicht die neuen Informationen von Router A mit den ihm bekannten Informationen ab und fügt schließlich seine Distanzvektorkosten (z.B. Anzahl der Hops) hinzu. Nun gibt Router B die „aktualisierte“ Routing-Tabelle an Router C weiter. Dieser Vorgang wiederholt sich bei jedem benachbarten Router.
Schritt für Schritt
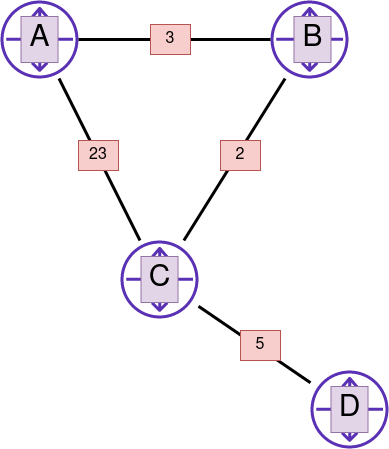
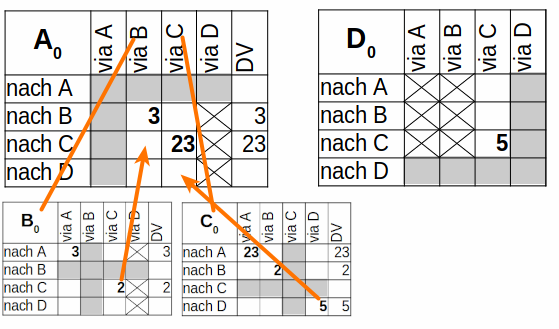
T=0: Knoten A erzeugt seine initiale Kostenmatrix. Sie enthält nur unsere direkten Nachbarn B und C mit den uns bekannten Kosten. Wir schicken daraufhin unsere neuen besten Pfade (B mit Kosten 3, C mit Kosten 23) an unsere direkten Nachbarn. Die anderen drei Knoten machen dasselbe aus ihrer Sicht.
T=1: Router A hat von den Routern B und C Datenpakete erhalten und weiß jetzt, zu welchen Kosten er D und wie er C und B jeweils auch erreichen könnte. Im Fall der Zielrouter C und D ist das sogar ein neuer bester Pfad. Im nächsten Schritt überträgt Router A diese Information wieder an seine Nachbarn. Alle anderen Knoten machen dasselbe.
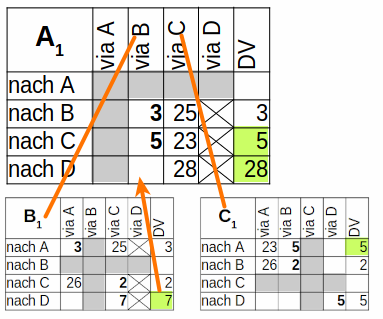
Damit ergibt sich nach dem ersten Schritt die folgende Situation.

(A1)
Vollziehe die Entstehung der Routingtabelle eines anderen Knotens (B,C oder D) nach. Von wem sind Infos beim Knoten angekommen? Welche Schlüsse können daraus gezogen werden?
T=2: Router A erhält wiederum von Router B ein neues Datenpaket und weiß jetzt, dass B den Router D günstiger erreichen kann. Wir tragen die Kosten in unsere Matrix ein und werden diesen neuen besten Pfad wieder an unsere Nachbarn verbreiten.
Nach Schritt 2 sieht die Situation also so aus:

Jetzt hat jeder Router eine Tabelle, aus der hervorgeht, welches der kürzeste Distanzvektor zu einem anderen Ziel im Netz ist und kann anhand dessen feststellen, an welchen Router er ein Datenpaket als nächstes schicken muss.

(A2)
Überprüfe, dass sich im Zeitschritt T=3 für die kürzesten Routen keine neuen Erkenntnisse mehr ergeben.

(A3)
Vollziehe nach dem Schema oben schrittweise nach, was auf Router A passiert wenn sich die Kosten der Verbindung zwischen B und C auf 25 erhöhen.
Material
Beispiel: https://de.wikipedia.org/wiki/Distanzvektoralgorithmus