Bäume: Einführung
Bäume dienen als hierarchisches Strukturierungsmittel oder als Organsisationsprinzip - ein Beispiel ist der nebenstehende Stammbaum, in dem Johannes Gans versucht, fast alle europäischen Herrscherdynastien auf die Nachkommenschaft Rudolfs von Habsburg zurückzuverfolgen.1)
Du kennst sicher weitere Beispiele, bei denen Daten und ihre Beziehungen zueinander als Baum strukturiert werden können.

(A1)
Finde 3 weitere Beispiele für baumartig strukturierte Daten und Zusammenhänge. Skizziere die jeweiligen Bäume in deinem Heft.
Allgemeine Begriffe
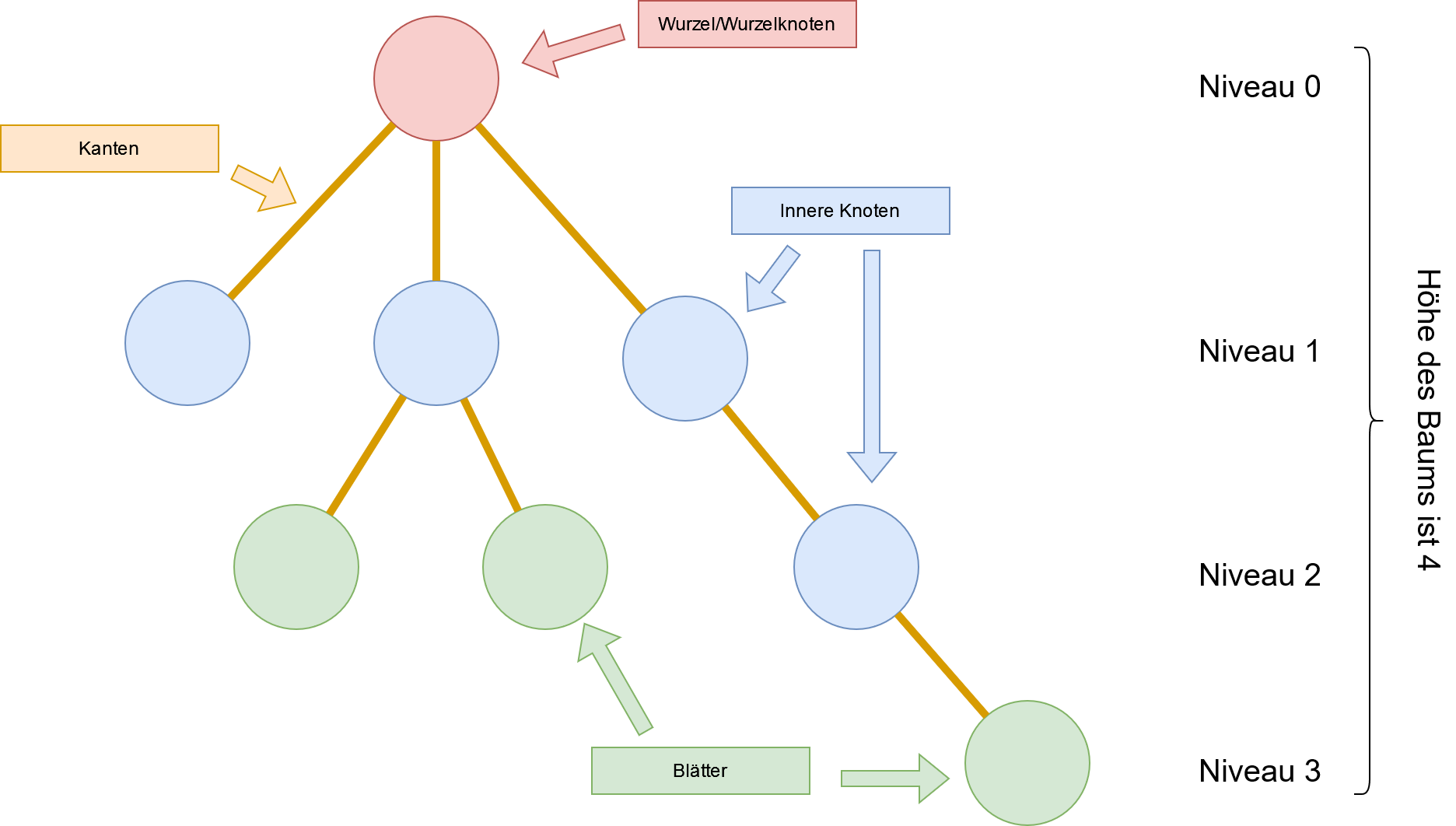
Allgemein besteht ein Baum (in der Informatik) aus Knoten und Kanten. Die Knoten sind teilweise durch Kanten verbunden. Damit wir von einem Baum sprechen, dürfen die Knoten allerdings nicht in beliebiger Weise untereinander verbunden sein, sondern es müssen bestimmte Regeln eingehalten werden:
- Jeder Knoten - außer dem Wurzelknoten - ist durch genau eine Kante mit seinem Elternknoten (Vaterknoten, Vorgänger) verbunden. Dieser Knoten wird häufig Kind oder Nachfolger des Elternknotens genannt.
- Der Knoten ohne Elternknoten ist der Wurzelknoten. Jeder (nicht-leere) Baum hat genau einen Wurzelknoten.
- Ein Knoten der keine Kinderknoten hat heißt Blatt.
- Knoten mit Eltern- und Kinderknoten heißen innere Knoten des Baums
- Ein Pfad ist eine Abfolge von Knoten, die durch Kanten miteinander verbunden sind. Bei einem Baum gibt es zwischen dem Wurzelknoten und jedem anderen Knoten genau einen Pfad. (Bäume sind "zyklenfrei" und "zusammenhängend").
- Das Niveau eines Knotens ist die Länge des Pfads vom Wurzelknoten zum betrachteten Knoten.
- Die Höhe des Baums ist die Anzahl der Knoten im längsten Pfad des Baums (oder gleichbedeutend: Das größte Niveau eines Knotens im Baum +1)
- In der Informatik zeichnet man Bäume aus praktischen Erwägungen von oben nach unten.
Wenn vorgegeben ist, welche (Maximal-)Zahl von Kinderknoten ein Knoten eines Baums haben darf, spricht man von einem n-ären Baum. Wenn die Kinder eines Knotens in einer bestimmten Reihenfolge geordnet sein müssen ("zuerst das linke Kind, dann das rechte"), spricht man von einem geordneten Baum.
Binärbaum
Ein sehr wichtiger Sonderfall, den wir im Weiteren betrachten werden ist der "2-äre" Baum, besser bezeichnet als binärer Baum oder Binärbaum.
- Bei einem Binärbaum hat jeder Knoten höchstens 2 Kindsknoten
- Es ist unterscheidbar, welches der linke und welches der rechte Kindsknoten ist.

(A2)
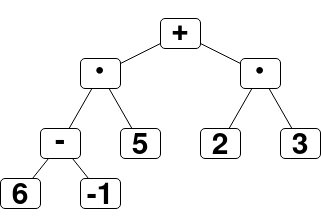
Bäume können dazu genutzt werden, Rechenausdrücke darzustellen, so dass sich Rechenregeln wie "Punkt vor Strich" in der Struktur wiederfinden.
- Welcher Term ist durch den Baum rechts dargestellt?
- Welche Höhe hat der Baum?
- Was ist das größte Niveau eines Knotens in diesem Baum?
- Handelt es sich um einen Binärbaum? Muss es sich um einen Binärbaum handeln, damit man Terme darstellen kann?
- Muss der Baum geordnet sein? Begründe?
- Skizziere den Baum für den Term
(9+2-3)*3+7/(6-2)
Material
| Filename | Filesize | Last modified |
|---|---|---|
| 01einfuehrung_baeume.odp | 166.1 KiB | 07.02.2022 18:15 |
| 01einfuehrung_baeume.pdf | 165.1 KiB | 07.02.2022 18:15 |
| baumbegriffe.drawio.png | 173.1 KiB | 14.01.2024 11:40 |
| bb_rollenspiel.odp | 95.7 KiB | 30.04.2024 11:25 |
| bb_rollenspiel.pdf | 60.2 KiB | 30.04.2024 11:25 |
| binaerbaum_rolenspiel.odt | 24.5 KiB | 30.04.2024 11:25 |
| binaerbaum_rolenspiel.pdf | 91.6 KiB | 30.04.2024 11:25 |
| stammbaum_habsburg_baden.jpg | 147.9 KiB | 07.02.2022 14:18 |
| term.drawio.png | 8.9 KiB | 07.02.2022 15:10 |