Der Call-Stack und die Rekursion
Ein populäres Beispiel für rekursive Algorithmen ist die Fakultätsfunktion:
5! = 5*4*3*2*1 fakultaet(5) = 120 fakultaet(3) = 3*2*1 = 6
(A1) Iterativ
Implementiere in BlueJ eine iterative Version der Fakultätsfunktion, die als Argument die Zahl entgegennimmt, deren Fakultät berechnet werden soll.
(A2) Rekursiv
Implementiere anhand des folgenden Pseudocodes eine rekursive Version fak_rekursiv.
fak_rekursiv(int n):
wenn n=1 oder n=0:
return 1
sonst:
return n*fak_rekursiv(n-1)
- Was ist der Rekursionsfall, was der Basisfall?
- Teste deine rekursive Methode
Dataillierte Betrachtung des Call-Stacks bei der Rekursion
| Was passiert | Wie sieht der Stack aus? |
|---|---|
fak_rekursiv(3) wird aufgerufen.Auf dem Stack wird Speicher für diesen Aufruf reserviert. Es gibt keine Rücksprungadresse. Innerhalb dieses Aufrufs wird fak_rekursiv(2) (nächster Schtritt) aufgerufen,da die Fallunterscheidung nicht zum Basisfall führt sondern zum Rekursionsfall. |  |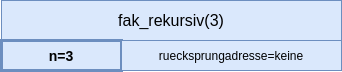
fak_rekursiv(2) wird aus dem vorhergehenden Aufruf heraus aufgerufen.Auf dem Stack wird Speicher für diesen Aufruf reserviert: Wichtig: Jeder Aufruf hat seinen eigenen Speicherbereich für Variablen, d.h. jeder Aufruf von fak_rekursiv hat sein eigenes n auf die die anderen Aufrufenicht zugreifen können. Die Rücksprungadresse befindet sich jetzt im vorigen Aufruf der rekursiven Methode selbst. Das ist anders, als beim ersten Beispiel für den Call-Stack! Da erneut der Rekursionsfall eintritt, wird aus diesem Aufruf heraus fak_rekursiv(1) aufgerufen. |  |
fak_rekursiv(1) wird aus dem vorhergehenden Aufruf heraus aufgerufen.Auf dem Stack wird Speicher für diesen Aufruf reserviert. Die Rücksprungadresse befindet sich wiederum im vorigen Aufruf der rekursiven Methode selbst. Jetzt tritt der Basisfall ein! |  |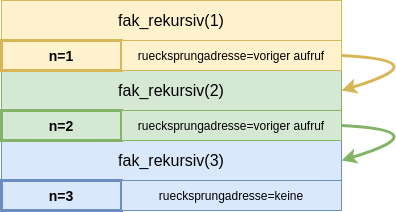
| Dies ist der erste Aufruf, der vollständig abgeschlossen ist. Es wird kein neuer Aufruf von fak_rekursiv auf den Call-Stack gelegt, sondernder Aufruf von fak_rekursiv(1) endet damit, dass 1 an dieaufrufende Stelle zurückgegeben wird und die zum Aufruf gehörenden Daten vom Stack entfernt werden. |  |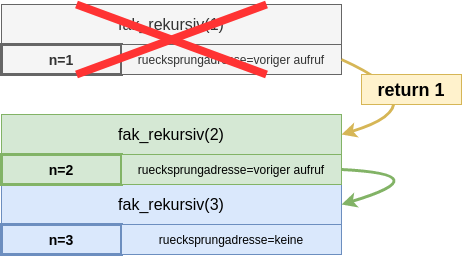
Damit hat der Aufruf von fak_rekursiv(2) alle Informationen,um abgeschlossen zu werden: Der Ausdruck n*fak_rekursiv(n-1) kann jetzt zu 2*1 ausgewertet und an dieaufrufende Stelle zurückgegeben werden. Die zum Aufruf gehörenden Daten werden vom Stack entfernt. |  |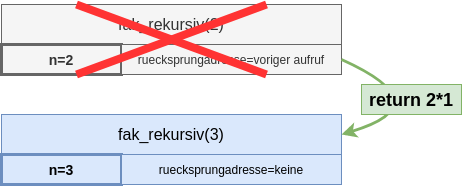
Jetzt hat auch der Aufruf von fak_rekursiv(3) alle Informationen,um abgeschlossen zu werden: Der Ausdruck n*fak_rekursiv(n-2) kann jetzt zu 3*2 ausgewertet und an die aufrufende Stelle zurückgegeben werden. Die zum Aufruf gehörenden Daten werden vom Stack entfernt. Der Call-Stack ist leer, der Aufruf der Methode beendet. |  |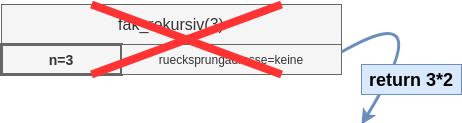
Zusammenfassung
- Rekursion bedeutet, dass eine Funktion/Methode sich selbst aufruft.
- Alle rekursiven Funktionen haben eine Fallunterscheidung: den Basisfall und den Rekursionsfall.
- Die Funktionsaufrufe werden auf dem Aufruf-Stack gespeichert, dabei wird dieser immer größer bis der Basisfall eintritt. Anschließend wird der Stack von oben nach unten "abgearbeitet", bis er leer ist und damit der Aufruf der rekursiven Methode endet.
- Der Aufruf-Stack kann unter Umständen sehr groß werden und sehr viel Arbeitsspeicher belegen.