Die Türme von Hanoi

Das Problem beim Turm von Hanoi besteht in der folgende Aufgabe:

1. Gegeben ist ein Turm auf einem Standplatz A aus n Scheiben, die übereinander liegen, und zwar immer eine kleinere auf einer größeren Scheibe.
2. Der Turm soll auf einen zweiten Platz B umgesetzt werden, wobei aber beim Umsetzen immer nur eine kleinere auf eine größere Scheibe gelegt werden darf. Es darf stets nur eine Scheibe bewegt werden.
3. Bei der Umsetzung darf ein dritter Hilfsplatz C mitbenutzt werden.

Du kannst das Spiel hier ausprobieren: https://www.mathematik.ch/spiele/hanoi_mit_grafik/

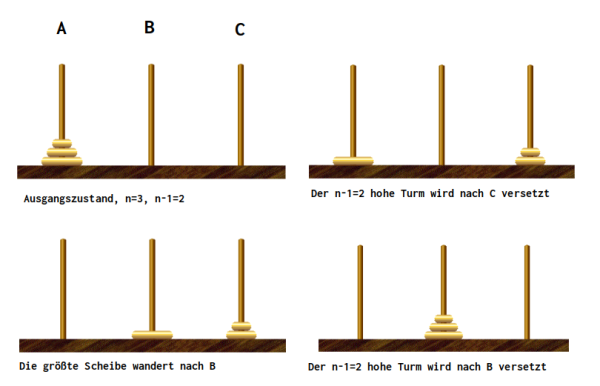
Bei genauerer Analyse des Problems, kann man erkennen, dass es rekursiver Natur ist: Beim Umsetzen des Turms mit n Scheiben vom Platz A zum Platz B muss man immer zunächst den Turm mit n-1 Scheiben, der sich auf der größten (untersten) Scheibe befindet, auf den "Hilfsplatz" C umsetzen.

Dann kann man die größte Scheibe nach B setzen und muss anschließend nochmal den n-1 großen Turm von C nach B umsetzen.

Vollziehe den rekursiven Charakter des Problems in der Simulation nach, indem du Türme mit 1,2,3,4 Scheiben umsetzt und dir dabei klar machst, dass du jeweils auf das Verfahren des vorigen Schritts mit n-1 Scheiben zurückgreifen kannst.

Modelliere das Problem in Java. Als ADT kannst du einen Stack verwenden, den es in der Java Standardbibliothek gibt:

import java.util.Stack;
[...]
public class Hanoi {
    int numDiscs;
    Stack<Integer> towerA = new Stack<>();
    Stack<Integer> towerB = new Stack<>();
    Stack<Integer> towerC = new Stack<>();
[...]
public Hanoi() {
// ersten Stapel füllen
}
 
// schiebe Turm von ... nach ...
public void move([...]) {
 
}
 
// alle drei Türme ausgeben
public void printState() {
 
}

• Implementiere den Konstruktor, der den Turm mit n Scheiben auf Platz A aufbaut.
• Implementiere zunächst die Methode printState(), die den Zustand des Spiels ausgibt.
• Implementiere die Rekursive Funktion move. Überlege, welche Argumente die Methode benötigt.

• Hier findet sich ein BlueJ-Projekt mit einem Codegerüst.
• Die Türme werden durch Stacks von Integern repräsentiert. Die einzigen benötigten Stack-Methoden sind push (lege ein Element auf den Stack) und pop (entferne das oberste Element vom Stack).
• Überlege dir beim Programmieren der Methode init(), durch welche Zahlen du die Scheiben repräsentieren willst.
• Die Methode moveTower() ist der eigentliche Algorithmus, der einen beliebige Anzahl Scheiben von einem Turm zu einem anderen Turm versetzt. Überlege dir einen Basis- und einen Rekursionsfall!
• Die Methode test() kannst du nutzen, um deine moveTower-Methode zu testen.
• Beachte: Beim Ausgeben eines Stacks (printState) ist das rechte Element des Stacks das oberste!