Sierpinski-Dreieck

Ein einfaches Sierpinski-Dreieck setzt sich rekursiv aus drei gleichseitigen Dreiecken halber Seitenlängen zusammen solange die Seitenlängen größer als eine minimale Länge m sind:

Im Folgenden soll zunächst die Methode zeichneSierpinskiGleichseitig(int laenge, int m) implementiert werden. Die Grundseite der Dreiecke soll dabei parallel zur x-Achse ausgerichtet sein.

Verwende weiter die Vorlage aus der Einführung in die Turtle Grafik.

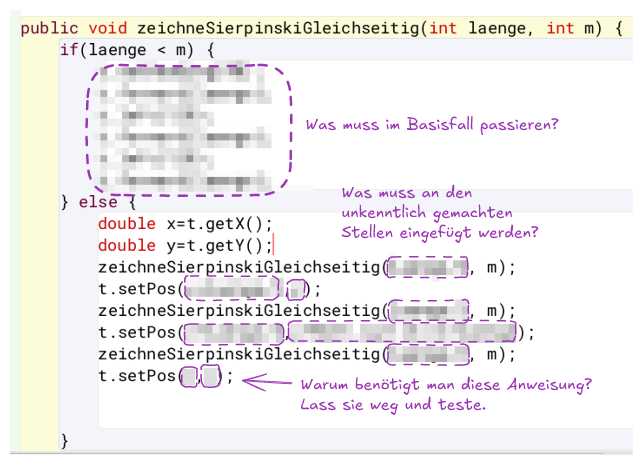
• Welche Bedingung ist maßgeblich, dass der Basisfall eintritt. Was muss dann geschehen?
• Wenn der Basisfall nicht zutrifft, müssen drei Dreiecke gezeichnet werden, indem sich die Methode rekursiv selbst aufruft. Vor jedem Aufruf muss der Startpunkt neu berechnet werden und die Turtle mit t.setPos(X,Y) an den berechneten Startpunkt gesetzt werden. Mit welchen Parametern muss sich die Methode selbst aufrufen?

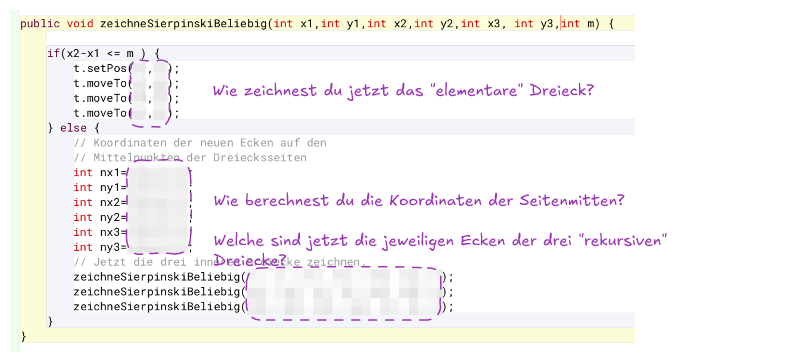
• Überlege dir, welche Bedingung hier den Basisfall definiert.
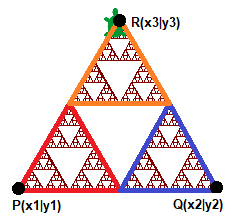
• Implementiere in deiner Methode, dass das Dreieck mit den Eckpunkten P(x1|y1), Q(x2|y2) und R(x3|y3) gezeichnet wird.
• Überlege dir, wie man die fehlenden Eckpunkte des roten, blauen und orangenen Dreiecks mithilfe der Koordinaten x1, y1, x2, y2, x3 und y3 in der Abbildung bestimmen kann.

Hilfestellung

• Ergänze deine Methode auf Basis dieser Überlegungen um geeignete Selbstaufrufe und implementiere die Methode. Geeignete Eckpunkte sind z.B. (0|0) (200|0) (100|174), eine geeignete minimale Seitenlänge für diese Koordinaten ist zwischen 5 und 10.