Bubble Sort

Oje, Willi hat seine Mistkugeln auf offenem Feld aufgereiht. Ein heftiger Windstoss und die Kugeln rollen davon und liegen schon wieder in einem Durcheinander. Also nochmals sortieren. Willi ist noch ganz erschöpft von seiner ersten Sortier-Aktion. Vor allem das Suchen der "falschen" Paare war sehr anstrengend! Er musste dabei immer die ganze Kugelreihe überblicken.

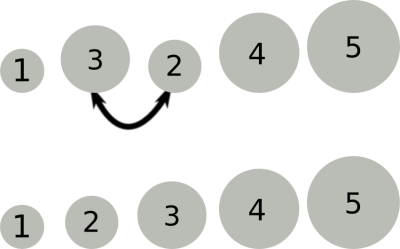
Gut, ich machs nochmals, sagt er sich, aber diesmal ein bisschen systematischer. Er sucht die "falschen" Paare jetzt nicht mehr nach dem Zufallsprinzip, sondern geht von links nach rechts durch die Reihe. Dabei vergleicht er immer zwei benachbarte Kugeln. Sobald er zwei Kugeln mit falscher Reihenfolge gefunden hat, vertauscht er diese. Nachdem er die ganze Reihe so abgearbeitet hat, beginnt er wieder vorn vorne, d.h. von links. Wenn es schon mit Zufall geklappt hat, denkt sich Willi, dann muss es doch mit System erst recht klappen. Vielleicht sogar noch schneller als vorher? Tatsächlich findet er nach einigen Durchgängen kein "falsches" Paar mehr…

Erster Durchlauf: Es wird von links nach rechts jeweils die Mistkugel mit ihrem rechten Nachbarn verglichen. Ist die rechte größer als die Linke, passiert nichts, ist die Linke größer als die rechte werden die beiden vertauscht. → 3 ist kleiner als vier, O.K., weiter zum 2. Element → 4 ist größer als 1, Tauschen. Weiter zum nächsten Element, dem dritten - nach dem Tausch ist das wieder die 4! → 4 ist kleiner als 5, O.K., weiter zun nächsten Element → 5 ist größer als 2, Tauschen. Weitergehen zu ELement vier. Durchlauf zu Ende.
Zweiter Durchlauf: → 3 > 1, Tauschen → 3 < 4, O.K. → 4 > 2, Tauschen → 4 < 5, O.K.
Dritter Durchlauf: → 1 < 3, O.K. → 3 > 2, Tauschen → 3 < 4, O.K. → 4 < 5, O.K.

Bei einem vierten Durchlauf würde man keine Vertauschung mehr benötigen - die Mistkugeln sind sortiert.

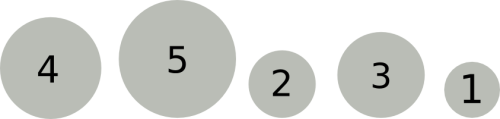
Sortiere auf einem Blatt Papier mit dem BubbleSort Verfahren die folgende Mistkugelreihe. Fertige eine Tabelle an, in der jeder Durchlauf des Sortierverfahrens zu erkennen ist, markiere die Vertauschungen.¹⁾

Beobachte die Postion der jeweils größten Kugeln, die noch nicht an ihrem endgültigen Platz sind - was fällt dir auf?

Wir sehen im Beispiel oben sofort, dass die Reihe nach dem dritten Durchgang sortiert ist und wir damit fertig sind. Wie aber kann ein Programm herausfinden, ob eine Reihe sortiert ist? Um zu entscheiden, ob die Reihe sortiert ist, kann unser Programm also einen weiteren Durchgang ausführen. Wenn in einem Durchgang kein "falsches" Paar mehr gefunden wird, sind wir fertig.

Diese Überlegungen führen uns auf folgenden Algorithmus:

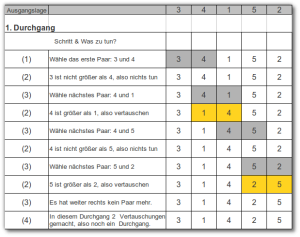
In der Datei sortieren_bubble.pdf (ODS) ist der erste Durchgang gemäß des Algorithmus notiert. Fülle die Tabelle vollständig aus:

• Schreibe stichwortartig in die Felder, welchen Schritt des Algorithmus man ausführt und was genau dabei gemacht wird.
• Notiere die Zahlenreihe und markiere bei jedem Schritt, welche Zahlen dort betrachtet werden.

Warum sind vier Durchläufe nötig? Erkläre!

• Erstelle eine Methode bubblesort in der Klasse Musikliste, die den Bubblesort-Algorithmus implementiert, um die Liste nach den Ratings zu sortieren. Es kann nötig sein, in der Klasse Song noch entsprechende getter-Methoden zu implementieren.
• Zähle, wie viele Durchläufe durch alle Songs der ArrayList nötig sind, bis die Liste sortiert ist.
• Lass dir die sortierte Liste ausgeben, um das Ergebnis zu kontrollieren.