Aufwandsabschätzung im Detail
Im Abschnitt zur binären Suche haben wir uns bereits einige Gedanken zur Aufwandsabschätzung gemacht.
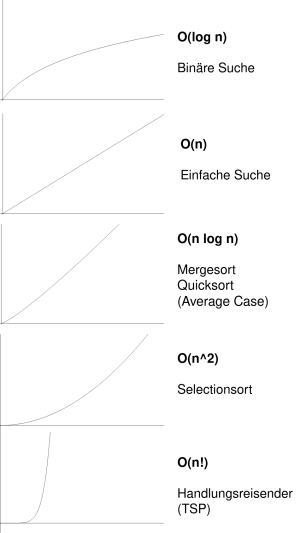
Um ein Gefühl dafür zu bekommen, was die gängigsten Laufzeitcharakteristiken bedeuten, können die folgenden Beispiele dienen:
| 10 Elemente | 100 Elemente | 1000 Elemente | |
|---|---|---|---|
| O(log n) | 0,15 Sekunden | 0,3 Sekunden | 0,5 Sekunden |
| O(n) | 0,5 Sekunden | 5 Sekunden | 50 Sekunden |
| O(n log n) | 1,6 Sekunden | 33 Sekunden | 490 Sekunden |
| O(n2) | 5 Sekunden | 8 Minuten | 14 Stunden |
| O(n!) | 2,1 Tage | 1,4*10149 Jahre | 0,6*102559 Jahre |
Hypothetisch wurden für diese sehr grobe Berechnung eine Bearbeitungsgeschwindigkeit von ca. 20 Operationen je Sekunde zugrunde gelegt, was natürlich sehr viel langsamer ist, als ein Computer real arbeitet.
Es ist aber wichtig zu verstehen, dass bei Problemen der Kategorie O(n2) oder gar O(n!) keine Rolle spielt: Wenn die Anzahl der Elemente wächst, wächst der Aufwand schneller als jede Rechenleistung das zu kompensieren vermag1).
Quicksort
Eine Besonderheit des Quicksort-Algorithmus ist, dass er Aufwand von der Wahl des Pivotelement abhängt.
Das hast du vielleicht bei deinen Übungen bereits bemerkt: Wenn man das Element stets sehr ungünstig wählt, gewinnt man beim Aufteilen des Problems kaum etwas. Die nach der Partitionierung größte zu sortierende Menge ist im schlechtesten Fall in jedem Rekursionsschritt nur ein Element kleiner als zuvor, wobei die kleinste Menge immer leer ist.
Quicksort hat im Worst Case eine Laufzeit von O(n2), im Average Case eine Laufzeit von O(n log n)
Aber was bedeutet Worst Case und Average Case genau?
Die Landau Notation im Detail
Faktoren spielen keine Rolle?
Die Landau Notation unterschlägt Konstanten - wenn man schreibt O(n) meint man eigentlich O(c*n). Das kann man sich am Beispiel eine Methode klar machen, die die Elemente eines Arrays ausgibt:
printArray(array):
für jedes Element element von array:
print element
Diese Methode hat die Laufzeit O(n) - sie muss jedes Element einmal anfassen uns ausgeben, bei doppelt so vielen Elementen dauert das doppelt so lange.
Jetzt betrachten wir die folgende Methode (Pseudocode):
printArrayMitPause(array):
für jedes Element element von array:
print element
warte(10s)
Die Methode printArrayMitPause benötigt sehr viel länger, um das Array auszugeben, da sie zwischen der Ausgabe zweier Arrayelement immer eine Pause von 10 Sekunden macht. Sie hat also gewissermaßen die Laufzeit 10Sekunden * n. Dennoch hat auch sie in der Landau-Notation die Laufzeit O(n), da man die Konstante (hier: 10 Sekunden) vernachlässigt!
Darf man das?
Suchvergleich mit Faktoren
Dazu vergleichen wir nochmal gedanklich die einfache Suche und die binäre Suche und ergänzen die Laufzeiten mit realen Zeitfaktoren:
| Einfache Suche | Binäre Suche |
|---|---|
10 Millisekunden * n | 1 Sekunde * log n |
Die einfache Suche läuft also beispielsweise auf einem sehr viel schnelleren Rechner, so dass pro Element lediglich 10 Millisekunden hinzukommen - die binäre Suche läuft auf einem langsameren Rechner, die Zeit wächst hier zwar logarithmisch aber mit einem Faktor von 1 Sekunde.
Dieser Vorteil wird jedoch von einer großen Anzahl von Elementen zunichte gemacht.

(A1)
Wie lange dauert es, eine Liste mit 4 Milliarden Elementen mit den beiden Algorithmen zu durchsuchen?
Wenn die Anzahl der Elemente veränderlich ist, spielen Faktoren bei der Landau Notation keine Rolle. Jeder Vorteil eines Faktors wird bei einem Algorithmus mit besserer Laufzeit bei genügend großer Anzahl der Elemente wieder eingeholt.
Faktoren spielen doch eine Rolle?
Manchmal spielen Faktoren aber eben doch eine Rollen - nämlich dann, wenn die Anzahl der Elemente beim Vergleich zweier Algorithmen vorgegeben ist. Das ist beispielsweise dann der Fall, wenn wir ein und dasselbe Array mit zwei unterschiedlichen Sortierverfahren sortieren wollen: Wenn die Laufzeit von Quicksort sich in Abhängigkeit des gewählten Pivotelements verändert, spielt der Faktor eine Rolle.
Die Konstante von Quicksort ist kleiner als die von Mergesort. Wenn beide Algorithmen eine Laufzeit von O(n log n) benötigen, ist Quicksort also schneller, wenn sich bei einer festen Anzahl von Elementen aber die Laufzeit von Quicksort hin zu O(n2) verschiebt, kann es sein, dass Mergesort irgendwann schneller ist, weil Mergesort immer die Laufzeit O(n log n) hat.
Average Case und Worst Case bei Quicksort
Wie oben bereits angedeutet, ist es besonders ungünstig, wenn die Partitionireung bei Quicksort immer so ausfällt, dass das größte zu sortierende "Unterarray" lediglich ein Element weniger hat, als das Array im Rekursionsschritt zuvor. Besonders leicht kann man sich das klar machen, wenn man ein Array betrachtet, das bereits sortiert ist und stets das erste Array-Element als Pivotelement wählt:
Worst Case
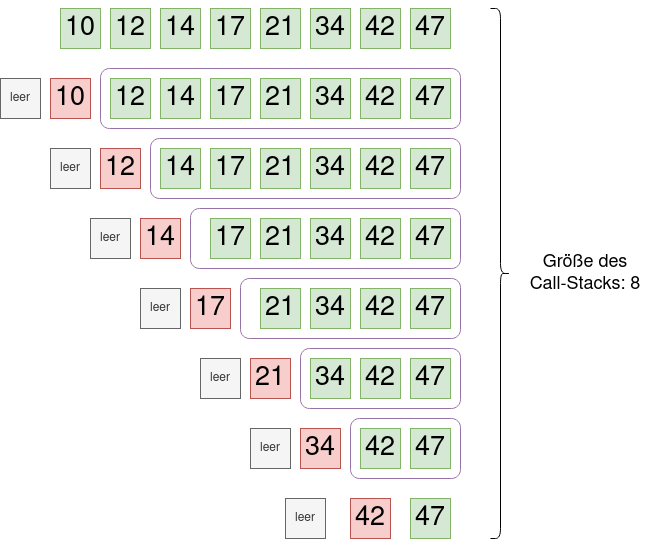
Wenn man den Sortiervorgang nachvollzieht, wenn man jeweils das erste Element des Arrays mit den größeren Elementen als Pivotelement wählt, sieht das so aus:
Auf jeder Ebene des des Call Stacks muss man alle Elemente betrachten um zu partitionieren - unabhängig vom gewählten Pivotelement. Das bedeutet, die Bearbeitung jeder Ebene des Call Stacks benötigt den Aufwand O(n).
Im Worst Case haben wir also n Ebenen, die jeweils mit dem Aufwand O(n) bearbeitet werden müssen - im schlechtesten Fall hat Quicksort also die Laufzeit O(n*n) also O(n2).
Best Case/Average Case
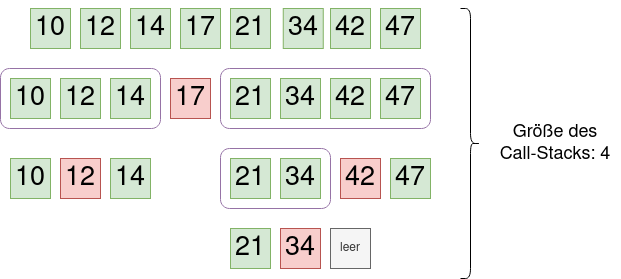
Wir wählen bei unserem sortierten Beispielarray jetzt immer das mittlere Element als Privotelement und schauen, was dann passiert:
Die Größe des Call Stacks ist hier nur 4 – oder allgemein (analog zur binären Suche) von der Ordnung log n. Auch hier gilt natürlich, dass wir auf jeder Ebene des des Call Stacks alle Elemente betrachten muss um zu partitionieren - unabhängig vom gewählten Pivotelement, also auch hier: Die Bearbeitung jeder Ebene des Call Stacks benötigt den Aufwand O(n).
Da es aber nur log n Ebenen gibt, ist der Aufwand von Quicksort im Best Case O(n * log n) also O(n log n)
Wenn du immer ein zufälliges Element des Arrays als Pivotelement auswählst, beträgt die Laufzeit von Quicksort auch im Durchschnitt O(n log n): Der Average Case ist der Best Case.

(A2)
Welche Laufzeiten haben die folgenden Operationen? Gib die Landau-Notation an und begründe deine Entscheidung kurz.
- Ausgabe der Werte aller Elemente in einem Array.
- Verdoppeln der Werte aller Elemente in einem Array.
- Verdoppeln des Werts des ersten Elements in einem Array.
- Erzeugen einer Multiplikationstabelle mit allen Elementen in einem Array. Es soll jedes Array-Element mit jedem anderen multipliziert werden.