Mergesort
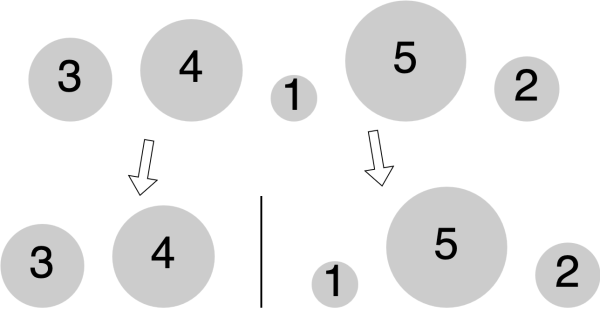
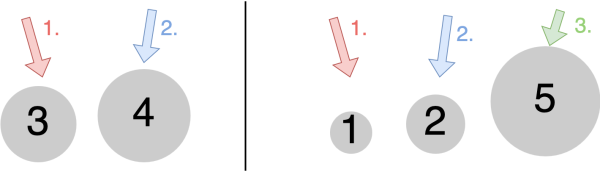
Nachdem der Mistkäfer Willi nun bereits so viele Sortierverfahren ausprobiert hat, ist er fix und fertig. Er ist nicht mehr imstande so viele unsortierte Mistkugeln in einem Rutsch abzuarbeiten. Daher überlegt er sich, dass es doch viel schöner wäre, wenn man das Problem vereinfachen könnte. "Ich möchte nicht direkt 5 Kugeln sortieren, sondern lieber 3 und 2 Kugeln separat voneinander. Danach kann ich diese zwei sortierten Teile immer noch wieder zusammenfügen." Und selbst diese 3 Kugeln sind Willi noch zu viel. Er unterteilt auch die 3 Kugeln wieder in 2 Kugeln und 1 Kugel, usw.
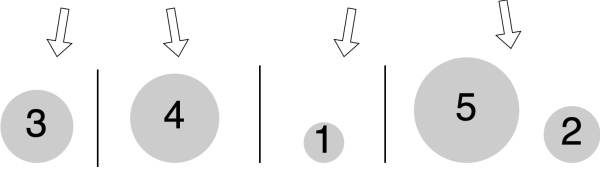
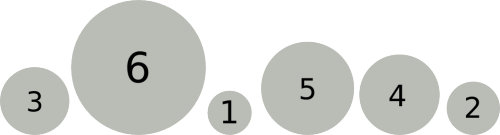
Irgendwann ist alles so weit unterteilt, dass Willi jeweils nur noch eine einzelne Mistkugel vor sich sieht. Dabei stellt er fest: "Das ist ja easy: die ist ja bereits sortiert!"
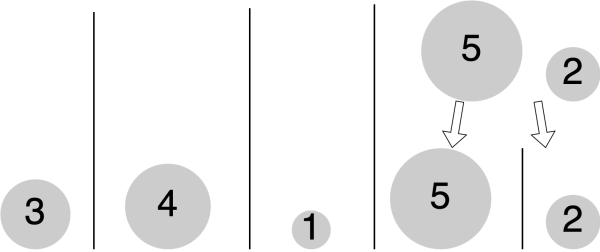
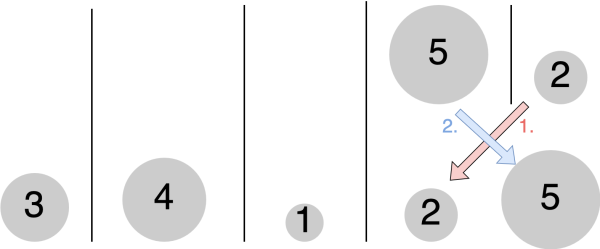
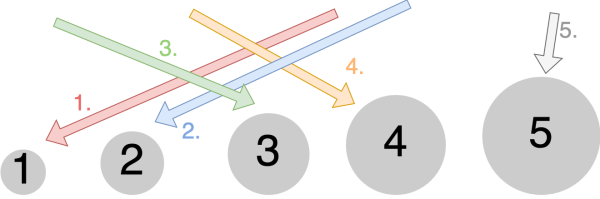
"Wenn ich nun jeweils zwei benachbarte und bereits sortierte Mistkugel-Bereiche wieder zusammenfüge, dann ist das ganz einfach, diese in die korrekte Ordnung zu bringen, denn die jeweils kleinste Zahl ist ganz vorne." Willi muss also nur jeweils die kleinste (=vorderste) Zahl aus den beiden benachbarten Bereichen vergleichen, die kleinere Zahl auswählen und in den neuen sortierten Bereich einfügen.
Schritt für Schritt
| Split-Phase: Das Array ist noch zu lang. Es wird mehrfach an der (abgerundeten) Hälfte halbiert, bis jedes Teilarray nur noch die Länge 1 hat. |  |
| Jedes Teilarray muss nochmal gesplittet werden… |  |
| Das hinterste Teilarray hat noch immer die Länge 2. Daher muss es nochmals halbiert werden. Damit ist das Ende der Split-Phase erreicht. |  |
| Merge-Phase (Verschmelzungsphase): Wir wissen nun, dass alle Teilarrays der Länge 1 jeweils offensichtlich sortiert sind. Nun fügen wir jeweils benachbarte Teilarrays in der korrekten Reihenfolge wieder zusammen. Dabei sollte die Reihenfolge beachtet werden, in der die Arrays zuvor aufgesplittet wurden. |  |
| Die beiden äußeren Teilarrays werden nun korrekt zusammengefügt. |  |
| Als letzter Merge-Schritt müssen nur noch die beiden letzten Teilarrays zusammengefügt werden. Hier ist gut sichtbar: man muss immer nur die beiden verbleibenden vordersten (=kleinsten) Zahlen der beiden Teilarrays miteinander vergleichen, um festzustellen, welche Zahl als nächste ausgewählt wird. Kleinschrittig: - Vergleiche die vordere 3 mit der vorderen 1. Wähle und entferne die 1, da diese kleiner ist. - Vergleiche die vordere 3 mit der vorderen 2. Wähle und entferne die 2, da diese kleiner ist. - Vergleiche die vordere 3 mit der vorderen 5. Wähle und entferne die 3, da diese kleiner ist. - Vergleiche die vordere 4 mit der vorderen 5. Wähle und entferne die 4, da diese kleiner ist. - Es bleibt nur noch die rechte 5 übrig. Wähle und entferne die 5. |  |
(A1)
Sortiere auf einem Blatt Papier mit dem MergeSort Verfahren die folgende Mistkugelreihe.
Algorithmus in Pseudocode
Anders als bei den vorherigen Algorithmen gibt es bei Mergesort nicht mehr zwei verschachtelte Schleifen. Mergesort und Quicksort nutzen Rekursion, um das große zu sortierende Array der Reihe nach in immer kleinere (und damit einfachere) Teilarrays zu zerlegen.
funktion mergesort(array);
falls (Länge von array <= 1) dann antworte array
sonst
halbiere die liste in linkesArray, rechtesArray
linkesArray = mergesort(linkesArray)
rechtesArray = mergesort(rechtesArray)
antworte merge(linkesArray, rechtesArray)
Die Methode merge(array1, array2) ganz am Ende kümmert sich nur darum, die beiden bereits sortierten Teilarray wieder in korrekter Reihenfolge zu einem Array zu "verschmelzen". Dies könnte man auch direkt innerhalb der Hauptmethode implementieren, es wird nur zugunsten der Übersichtlichkeit ausgelagert.
Wie bei rekursiven Vorgehensweisen üblich, umfasst der Code nur äußerst wenige Zeilen Code:
Die sichtbaren Zeilen in der Hauptmethode kümmern sich mit Ausnahme der letzten Zeile nur um das wiederholte Halbieren des Arrays bis nur noch eine Länge von 1 übrig bleibt (Basisfall der Rekursion).