Quicksort

Quicksort ist ein sehr schneller Sortieralgorithmus. Er kommt in der Praxis häufig zum Einsatz. Zahlreiche Standardbibliotheken verschiedener Programmiersprachen enthalten Methoden, um zum Beispiel Arrays zu sortieren, die in als Quicksort implementiert sind. Zum Beispiel hat die Standardbibliothek der Programmiersprache C eine Funktion namens qsort. Quicksort verwendet ein Teile-und-herrsche-Prinzip.

Stell dir vor, die Schüler der 7a wollen sich wie die Orgelpfeifen der Größe nach geordnet aufstellen:

Zunächst wählt man die erste Person als "Vergleichsgröße" aus, der Fachbegriff für das Element, das als Vergleichselement verwendet wird, ist Pivotelement.

Jetzt teilt man das Problem in zwei Unterprobleme auf: Alle Schülerinnen, die kleiner als das Pivotelement sind stellen sich links davon auf, alle die größer oder gleich sind rechts:

Das Pivotelement scheidet jetzt aus dem Verfahren aus, es bleibt an dem Platz, an dem es sich jetzt befindet. Jetzt haben wir zwei "kleinere" Sortierprobleme geschaffen: Die Schülerinnen, die links stehen sind ungeordnet, die größeren auf der rechten Seite ebenfalls. Auf jeden Fall – auch im ungünstigsten¹⁾ – sind die neuen Teilproblem(e) kleiner als das ursprüngliche Problem.

In den beiden Teilmengen verfährt man jetzt wie gerade in der Ausgangsmenge:

• Pivotelement wählen (die erste Schülerin ganz links)
• Menge in zwei Teile teilen: Kleiner und größer/gleich Pivotelement

Dieses Vorgehen wird jetzt wiederholt bis der Basisfall eintritt.

Führe das Verfahren mit Stift und Papier zu Ende, bis du die Schüler nach Körpergröße sortiert hast.

Frage: Was ist der Basisfall beim Sortieren der Schülergruppen? Wann kannst du also direkt ohne weitere Überlegung eine sortierte Schülergruppe zurückgeben?

Antwort:

Wir legen den Basisfall zugrunde: Wenn unser Array leer ist oder nur ein Element hat, ist es sortiert und kann direkt als sortiertes Array zurückgegeben werden:

public ArrayList<Integer> quicksort(ArrayList<Integer> listToSort) {
   if(listToSort.size() < 2) {
     return listToSort;
   }
   [...]
}

Arrays mit zwei Elementen sind ebenfalls einfach zu bearbeiten: Man muss lediglich die beiden Elemente vergleichen und wenn nötig vertauschen, bevor man das dann sortierte Array zurückgibt.

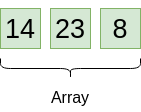
Spannend wird es, wenn das Array drei Elemente hat:

Wir gehen vor, wie oben angedacht:

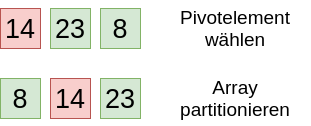
• Pivotelement wählen (erstes Element des Arrays)
• Partitionieren in Elemente kleiner als Privot, Pivot und Elemente größer/gleich Pivot:

Bislang haben wir als Pivotelemet stets einfach das erste Element des Arrays gewählt - tatsächlich ist es zunächst unerheblich, welches der Elemente man dazu heranzieht.

Untersuche, ob die Auswahl des Pivotelements einen Einfluss auf das Ergebnis des Sortiervorgangs hat, indem du das Verfahren mit jedem der Elemente als Pivotelement durchführst.

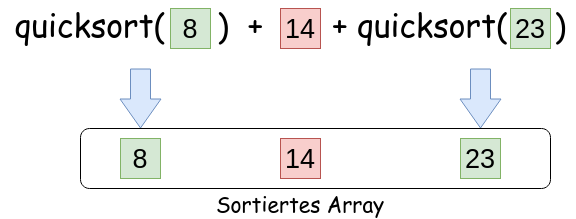
Das sortierte Array erhält man anschließend zuverlässig als:

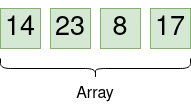
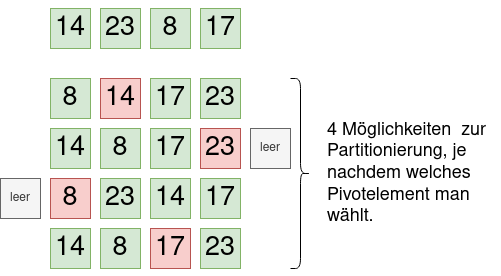
Betrachten wir nun ein Array mit 4 Elementen:

Gleichgültig, welches Element man als Pivot Element wählt, erhält man eine Partitionierung, die aus eine linken Array, den Pivot-Element selbst und einem rechten Array besteht. in manchen Fällen sind die linken oder die rechten Arrays leer, was aber kein Problem darstellt, da das durch unseren Basisfall abgedeckt ist.

Das längste dabei auftretende "Unterarray" hat zwangsläufig die Länge drei, das das Pivotelement selbst bei der Partitionierung "herausgenommen" wird. Ein Array der Länge drei können wir aber sortieren (s.o.)!. Wenn wir unsere Quicksort Methode also rekursiv mit einem Array der Länge drei aufrufen, stellt das kein Problem dar.

Diese Überlegung gilt nun analog für alle längeren Arrays: Nach der Partitionierung eines Arrays der Länge 5 hat das längste Unterarray die Länge 4. Wir wissen aber, dass wir ein Array der Länge 4 sortieren können (s.o.). Ein Array der Länge 6 hat nach der Partitionierung Unterarrays, die nicht länger als 5 sind, und so weiter.

Damit sieht der Quicksort-Algorithmus im Pseudocode folgendermaßen aus:

quicksort(array): array
  wenn laenge(array) < 2:
    return array
  sonst:
    pivot = array[0]
    array kleiner  = (Alle Elemente von Array, die kleiner sind als pivot)
    array groesser = (Alle Elemente von Array, die größer sind als pivot)
    return quicksort(kleiner) + pivot + quicksort(groesser)

Identifiziere im Pseudocode den Basisfall, den Rekursionsfall und die Partitionierung.

Verwende die Vorlage https://codeberg.org/qg-info-unterricht/array-summe. Implementiere dort die Methode quicksort in Java.

• Implementiere eine Methode kontrollausgabe(array), die es dir ermöglicht das Array vor und nach dem Sortieren zu betrachten
• Teste deine Methode mit unterschiedlichen Arrays - mit verschiedenen Wertebereichen und Längen. Kontrolliere die Ausgaben.

Implementiere eine Methode quicksort, im Musiklisten-Projekt (https://codeberg.org/qg-info-unterricht/musikliste-sortieren) um die Musikliste nach den Ratings zu sortieren.