Quicksort
Ein weiterer, sehr effizienter Algorithmus zum Sortieren großer Datenmengen ist Quicksort. Auch Quicksort findet sich in zahlreichen aktuellen Bibliotheksimplementationen moderner Programmiersprachen wieder. Quicksort wurde ca. 1960 von C. Antony R. Hoare in seiner Grundform entwickelt und seitdem von anderen Forschern verbessert.
Prinzip
- (Man vermischt das Array aus Performanzgründen)
- Man wählt das erste Element1) als Pivotelement und ordnet anschließend alle Elemente so an, dass das Pivotelement das Array in zwei Teile teilt: Die Elemente des ersten Teilarrays sind alle kleiner als das Pivotelement, die Elemente des zweiten Teilarrays sind alle größer als das Pivotelement.
- Anschließend verfährt man mit den Teilarrays rekursiv analog.
Teilen
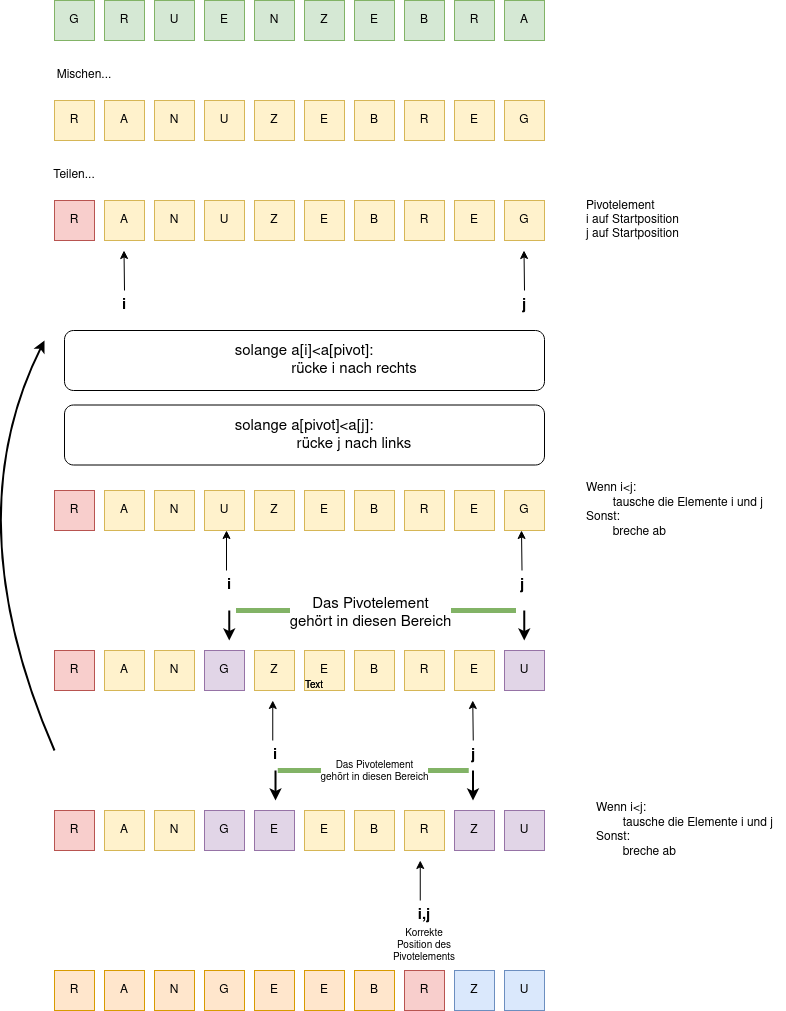
Im ersten Schritt teilt man das Array bezüglich eines Pivotelements in zwei Teile: Alle Elemente links des Pivotelements sollen kleiner sein als dieses, alle rechts davon größer.
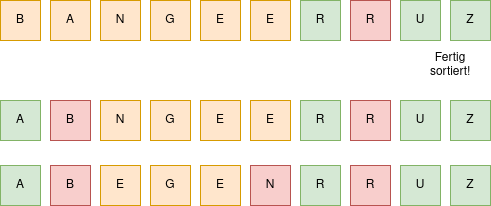
Nun kann man (letztlich rekursiv) das Verfahren auf die beiden Teilarrays (im Bild orange, bzw. blau) erneut anwenden.

(A1)
Führe das Verfahren für beide Teilarrays von Hand erneut aus, ohne erneut zu mischen. Vollziehe für das orange Teilarray 3 weitere Teilungsvorgänge nach. Warum machen drei weitere Teilungen beim blauen Teilarray keinen Sinn?

(A2)
Implementiere im BlueJ-Projekt in der Klasse Quicksort die Methode public int partition(String[] a, int li, int re), die ein gegebenes Array im Bereich von li bis re am Element an der Position li teilt.
Vom Teilen zum Quicksort
Verfügt man über eine funktionale "Teilen"-Methode, kann man Quicksort gemäß des folgenden Pseudocodes implementieren:
funktion sort(a, li, re)
falls li < re dann
tpos:= partition(a,li, re)
sort(a, li, tpos - 1)
sort(a, tpos + 1, re)
ende
ende

(A3)
Was ist der Basisfall bei diesem Rekursionsaufruf? Wie könnte man den Code schreiben, damit der Basisfall deutlicher sichtbar wird?

(A4)
Implementiere Quicksort in der Methode sort des BlueJ-Projektes. Achte darauf, dass die sort-Methode überladen werden muss, um die Abstrakte Methode sort aus der Klasse Sorting bereitzustellen.