Kompression mit Huffman-Codierung
Bei der herkömmlichen Text-Codierung mithilfe der ASCII-Tabelle besitzt jedes Zeichen eine Codelänge von genau 8 Bit. Die Idee hinter der Huffman-Codierung ist die, dass häufig vorkommende Zeichen mit einer kürzeren Codelänge auskommen als weniger häufig vorkommende Zeichen.
Ein Beispiel kennst du bereits: Morsecode verwendet als Code für das häufig vorkommende E lediglich ein • wohingegen ein Q in den den deutlich längeren Morsecode −−•− übersetzt wird.
Beim Morsen muss man neben den beiden Symbolen "kurz" und "lang" auch noch mit Pausen arbeiten, um die unterschiedlichen Zeichen unterscheiden zu können. Das ist nötig, da der Morsecode nicht präfixfrei ist, das bedeutet, dass es Codes von Zeichen gibt, die gleichzeitig auch als Anfang eines anderen Codes interpretiert werden können.
Beispiel: Das E mit seinem Code • ist gleichzeitig auch der Anfang des Zeichens A mit dem Code •−. Damit ist der Morsecode ohne zusätzliche Pause (also einem dritten Zeichen) nicht mehr eindeutig entzifferbar:
. - - . . . - . - .= ABC. - - . . . - . - .= EGFN
Der Huffman-Code bildet solch einen präfixfreien Code, der gleichzeitig den häufig vorkommenden Zeichen eine kürzere Codelänge generiert. Der Huffman-Code ist eine sogenannte Entropiekodierung.
Mithilfe der Seite https://cmps-people.ok.ubc.ca/ylucet/DS/Huffman.html lässt sich der Algorithmus schrittweise simulieren und visualisieren.
(A1)
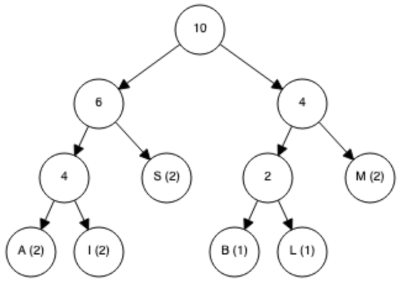
Lasse mit der Seite die Simulation für den Text „OTTOS MOPS KOTZT“ durchführen und beobachte den Aufbau des Baumes.1)
Erzeugung des Huffman Baums und des Huffman Codes
- Bestimme die Häufigkeit Hx aller vorkommenden Zeichen x.
- Erzeuge Knoten für jedes Zeichen x und markiere dieses mit der zum Zeichen gefundenen Häufigkeit Hx. Die Knoten werden in der Simulation als Kreise dargestellt.
- Nimm die beiden Knoten mit der geringsten Häufigkeit, die noch nicht verarbeitet wurden. Erzeuge einen neuen Knoten und hänge die beiden gefundenen an diesen an. Markiere den neuen Knoten mit der Summe der beiden Häufigkeiten der angehängten Knoten.
- Wiederhole 3. so lange, bis nur noch ein einzelner Knoten übrig bleibt, an dem sämtliche andere Knoten angehängt wurden.
- Markiere alle linken Kanten mit 0, alle rechten Kanten mit 1. Der Code für ein Zeichen x ergibt sich dann aus dem Weg vom Wurzelknoten bis zu diesem Zeichen.
Mobile-Modell für die Huffman-Codierung
- Bestimme die Häufigkeit Hx aller vorkommenden Zeichen x.
- Hänge die Zeichen als "Mobilefiguren" beginnend mit den am wenigsten häufigen Zeichen ans Mobile und achte darauf, dass das Mobile möglichst ausgeglichen ist. Die Präfixfreiheit ergibt sich dadurch, dass sich an den "Anbindepunkten" der Querstäbe keine Zeichen befinden können, damit sind alle inneren Knoten des Baums leer.
- Markiere alle linken Kanten mit 0, alle rechten Kanten mit 1. Der Code für ein Zeichen x ergibt sich dann aus dem Weg vom Wurzelknoten bis zu diesem Zeichen.
Weitere Übungen
(A2)
(A) Erzeuge aus dem Baum, den du oben generiert hast, die Codierung für jedes einzelne Zeichen (inklusive Leerzeichen) Anmerkung: Je nach Anordnung der Buchstaben und Knoten im Baum ist dieser Code nicht eindeutig.
Am besten machst du das in einer Tabelle:
| Zeichen | O | M | T | … |
| Häufigkeit | 4 | 1 | 4 | … |
| Code | 01 | … | … | … |
(B) Codiere den Text mit dem gefundenen Code. Wieviel Bit/Byte hat die ASCII Codierung des Textes in Anspruch genommen, wieviele Bit benötigt der Satz, wenn er mit dem Huffman-Code codiert wird?
(C) Welche Information benötigt ein Mitschüler, um deinen Code decodieren und den ursprünglichen Text wiederherstellen zu können?
(A3)
Für den Text "ABRACADABRA": Erzeuge von Hand den Huffman-Baum, erstelle daraus einen Huffman-Code und codiere damit den Text.
(A4)
(A5)
(A6)
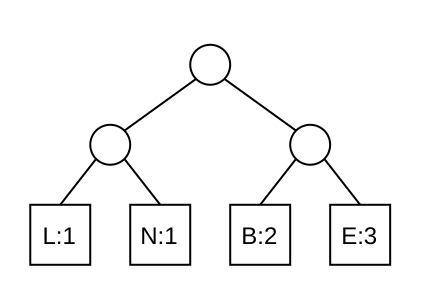
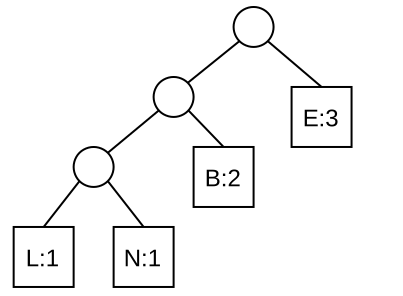
Gegeben ist der folgende Baum:
- Begründe, warum der Baum kein gültiger Huffman-Baum ist.
- Erläutere den Nachteil, der beim Codieren des Wortes "BELEBEN" mit diesem Baum auftritt.
- Gib einen korrekten Huffman-Baum für die angegebenen Buchstabenhäufigkeiten an.
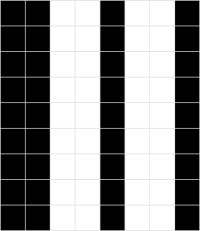
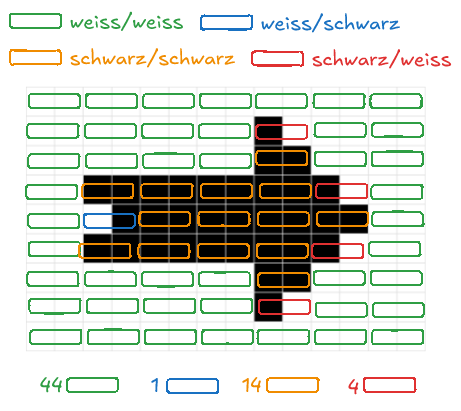
(A7) Bildkompression
Mit Hilfe einer "Zwischencodierung" kann man mit dem Huffman Code auch Bilder komprimieren. Betrachte das folgende Bild:
Untersucht man das Bild jetzt zeilenweise und betrachtet die folgenden 4 möglichen "Pixelpaare", kann man das Bild mit der Huffman-Codierung komprimieren:
| Pixelpaar | Weiß-Weiß | Weiß-Schwarz | Schwarz-Weiß | Schwarz-Schwarz |
|---|---|---|---|---|
| Wie oft? | ||||
| Code |
- Wie viele Bits benötigt man, wenn man die Bilddatei so codiert? Vergleiche mit der Bitweisen Codierung.
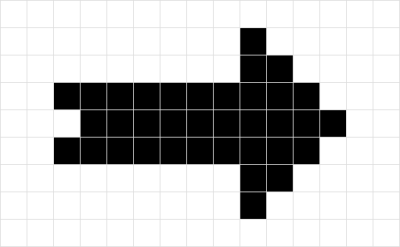
- Warum ist es nicht sinnvoll, das folgende Bild auf diese Weise zu komprimieren? Begründe!
Material
| Filename | Filesize | Last modified |
|---|---|---|
| 05-kompression_huffman.odp | 871.7 KiB | 29.11.2023 18:23 |
| 05-kompression_huffman.pdf | 770.5 KiB | 29.11.2023 18:23 |
| huff2.png | 10.9 KiB | 28.09.2022 16:00 |
| huff2lsg.png | 12.3 KiB | 28.09.2022 16:04 |
| huffb01.png | 79.7 KiB | 14.10.2021 16:14 |
| mobile.svg | 3.4 KiB | 29.11.2023 18:25 |
| pfeil.png | 5.5 KiB | 29.11.2023 18:51 |
| streifen.png | 5.1 KiB | 29.11.2023 19:01 |