Dörfer im Gebirge

Einige Dörfer in den Bergen sind über ein Straßennetz zu erreichen. Eine Hauptstraße führt zum ersten Dorf des Tales. Nach einem Unwetter sind einige Dörfer aber nicht mehr erreichbar und melden SOS.

Daraus lässt sich auf den Zustand der Straßen schließen. Es gibt drei Möglichkeiten:

• 1 = Die Straße ist nicht befahrbar
• 2 = Die Straße ist befahrbar
• 3 = Ohne weitere Information ist nicht entscheidbar, ob sie befahrbar oder nicht

befahrbar ist

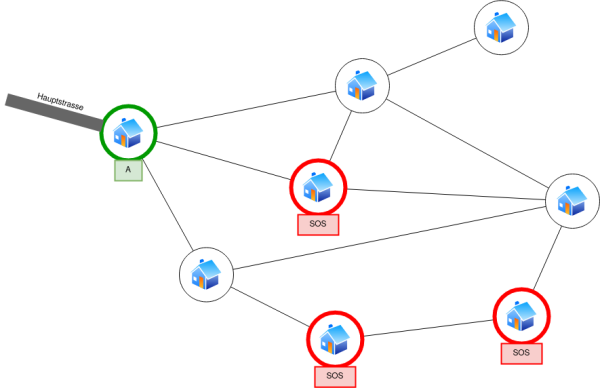
Die Hauptstraße ist immer befahrbar. Unten ist das Straßennetz abgebildet. Die Hauptstraße führt zu Dorf A ganz links oben.

(A) Gib für jede andere Straße ihren Zustand an.

Mit Hilfe des folgenden Algorithmus kann man den Zustand der Straßen automatisch ermitteln:

1. Setze alle Straßen auf "nicht entscheidbar".
2. Kennzeichne alle Straßen von einem unerreichbaren Dorf zu einem erreichbaren Dorf als "nicht befahrbar".
3. Für jede Straße S zwischen zwei erreichbaren Dörfern:
   1. Markiere S als "nicht befahrbar".
   2. Bestimme die Anzahl der Dörfer, die von Dorf A aus über "befahrbare" oder "nicht entscheidbare" Straßen erreichbar sind (inklusive A selbst).
   3. Stimmt die Anzahl mit der Anzahl der Dörfer ohne "SOS" überein, setze S auf "nicht entscheidbar". Andernfalls setze S auf "befahrbar".

(B) Begründe, warum eine Straße zwischen einem erreichbaren und einem nicht erreichbaren Dorf auf jeden Fall auf "nicht befahrbar" gesetzt werden muss.

(C) Erläutere die Breitensuche und wie sie in Schritt 3.b) zur Bestimmung der erreichbaren Dörfer eingesetzt werden kann.

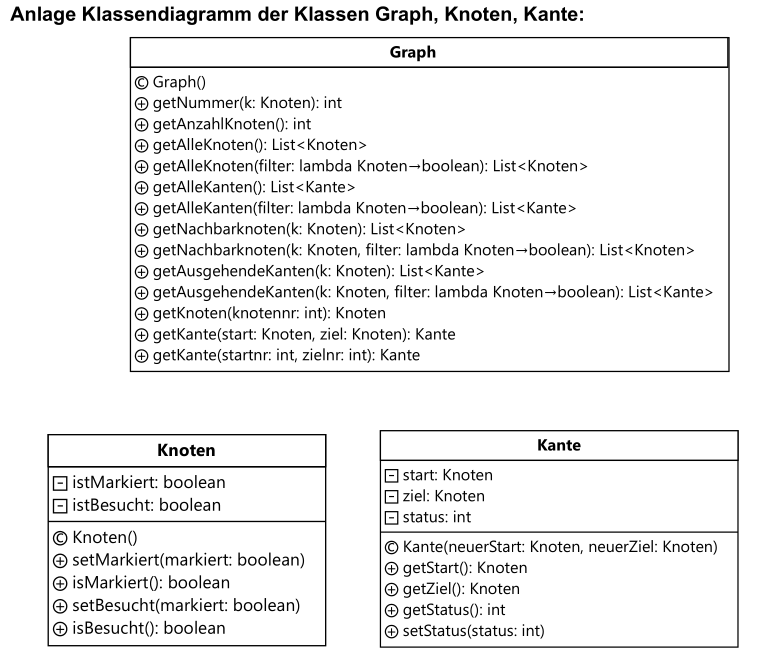
(D) Implementiere die Methode bestimmeStrassenzustaende(g: Graph, startknoten: Knoten), die den Straßenzustand aller Straßen als Status der Kanten im Graphen speichert. Knoten, die Städte mit "SOS" repräsentieren, sind markiert. Sie können davon ausgehen, dass die Methode bestimmeAnzahlErreichbare(startknoten: Knoten): int, die die Anzahl der erreichbaren Städte wie in Schritt 3.b) beschrieben bestimmt, schon fertig implementiert ist.