Einführung in die Datenstruktur Graphen
"Auf den Spuren eines Handelsreisenden"
Spielanleitung: https://www.youtube.com/watch?v=IDbbiNFjJeM
Was ist ein Graph?
Ein Graph ist ein Gebilde, das aus Knoten und Kanten besteht. Jede Kante verbindet zwei Knoten oder einen Knoten mit sich selbst. Von einem Knoten können eine, mehrere oder keine Kanten ausgehen. Formal schreibt man:
Graph
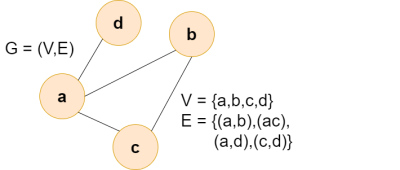
G = (V,E)mitV: Knotenmenge undE: Kantenmenge
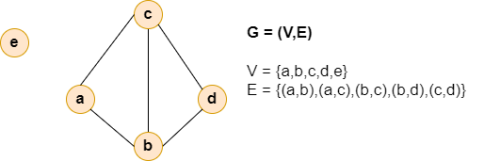
Das bedeutet so viel wie: "Ein Graph G ist ein Tupel (V,E), wobei V die Menge von Knoten (Vertices) und E die Menge von Kanten (Edges) des Graphen bezeichnet." Das Bild von einem Beispielgraphen rechts veranschaulicht dies.
 (1) Zeichne den folgenden Graphen:
(1) Zeichne den folgenden Graphen: V = {29,8,1,16,42,3} und E = {(8,42),(8,1),(16,8),(8,29),(1,16),(42,3),(29,42),(3,29)}.
Eigenschaften von Graphen
Multigraphen
Sind zwei Knoten durch mehrere Kanten verbunden, so spricht man von "Mehrfachkanten" und nennt die zugehörigen Graphen Multigraphen. Ein Graph ohne Mehrfachkanten wird als "einfacher Graph" bezeichnet.
 (2) Notiere, welche der folgenden Graphen Multigraphen sind.
(2) Notiere, welche der folgenden Graphen Multigraphen sind.

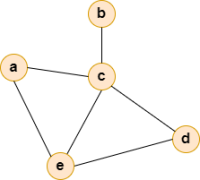
Der Grad eines Knotens (Knotengrad) ist die Anzahl der Kanten, die in diesem Knoten zusammentreffen. Im Graph rechts haben die Knoten folgende Grade:
| Knoten | Grad |
|---|---|
| a | 2 |
| b | 1 |
| c | 4 |
| d | 2 |
| e | 3 |
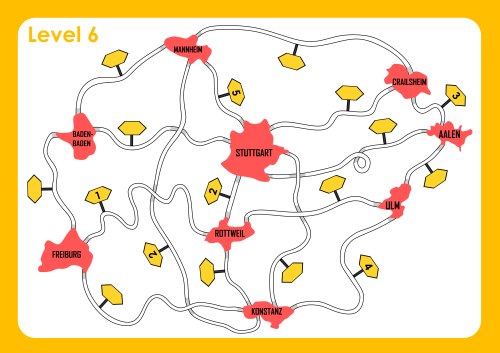
 (3) Ermittle den Grad aller Knoten des sechsten Levels aus dem Spiel "Auf den Spuren eines Handelsreisenden".
(3) Ermittle den Grad aller Knoten des sechsten Levels aus dem Spiel "Auf den Spuren eines Handelsreisenden".
Vollständigkeit
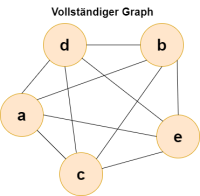
Ein Graph heißt vollständig, wenn jeder Knoten mit jedem anderen Knoten des Graphs durch eine Kante verbunden ist. Rechts ist ein Beispiel für einen vollständigen Knoten zu sehen.
 (4) Finde heraus, wie viele Kanten ein vollständiger Graph mit 3, 7 und mit 8 Knoten hat.
(4) Finde heraus, wie viele Kanten ein vollständiger Graph mit 3, 7 und mit 8 Knoten hat.
Richtung
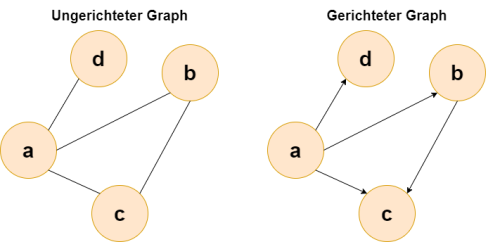
Die Kanten zwischen Knoten können eine Richtung haben, dann nennt man den Graph gerichtet. Die Richtung einer Kante wird durch eine Pfeilspitze am entsprechenden Ende angezeigt (siehe Abb. unten). Beispielsweise kann so die Fahrtrichtung einer Einbahnstraße angegeben werden.
Sind bei den Kanten keine Richtungen angegeben, nennt man den Graphen ungerichtet. Die Kante wird durch eine Linie dargestellt (siehe Abb. unten).
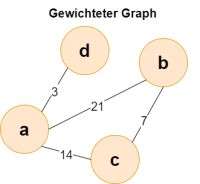
Die Kanten eines Graphen können gewichtet bzw. bewertet sein. Jeder Kante ist dann ein sogenanntes Kantengewicht zugewiesen (siehe Abb. rechts). Damit können zum Beispiel Kosten oder Entfernungen zwischen zwei Punkten (Knoten) dargestellt werden.
 (5) Das Traveling Salesman Problem ist ein typisches Beispiel für ein Problem auf einem gewichteten Graphen. Es handelt sich dabei um ein Problem, das sowohl im Alltag als auch in vielen anderen Bereichen seine Anwendung findet und immer wieder gelöst werden muss. Recherchiere weitere Anwendungsgebiete des TSP.
(5) Das Traveling Salesman Problem ist ein typisches Beispiel für ein Problem auf einem gewichteten Graphen. Es handelt sich dabei um ein Problem, das sowohl im Alltag als auch in vielen anderen Bereichen seine Anwendung findet und immer wieder gelöst werden muss. Recherchiere weitere Anwendungsgebiete des TSP.
Zusammenhängende Graphen
Ein Graph heißt zusammenhängend, wenn man entlang der Kanten von jedem Knoten zu einem anderen gelangen kann. Der Graph G auf der rechten Seite ist nicht zusammenhängend. Von Knoten a kann der Knoten e nicht erreicht werden.
 (6) Ergänze den Graphen G, sodass er zusammenhängend ist.
(6) Ergänze den Graphen G, sodass er zusammenhängend ist.
Wege in Graphen
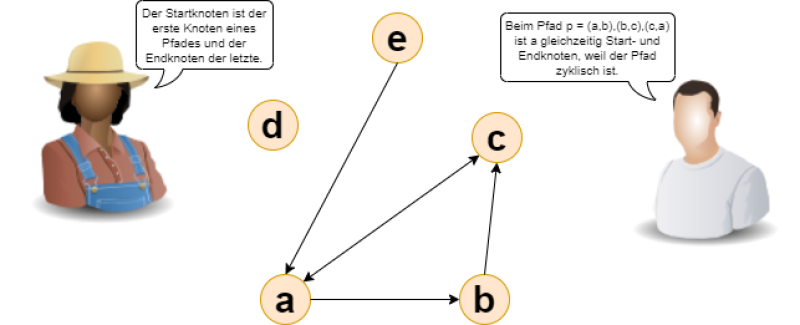
Einen Weg durch einen Graphen nennt man Pfad. Das ist eine endliche Folge von Kanten, die man durchlaufen muss, um von einem Startknoten zu einem Endknoten zu gelangen. Dabei gibt es zwei verschiedene Arten von Pfaden:
- Einfache Pfade, auch Wege genannt, durchlaufen keine Kante mehrfach.
- Zyklische Pfade (Zyklen/Kreise) sind geschlossen. Das bedeutet, dass sie den gleichen Start- und Endknoten haben.
Hier ist dies beispielhaft veranschaulicht:
 (7) Zeichne im Graphen aus Aufgabe (1) den Pfad
(7) Zeichne im Graphen aus Aufgabe (1) den Pfad p = (1,8),(8,42),(42,3),(3,29),(29,8) ein. Handelt es sich um einen einfachen oder einen zyklischen Pfad? Erkläre.
Ein Zyklus, der jeden Knoten eines Graphen genau einmal enthält, heißt Hamilton-Kreis. Diesen Begriff habt ihr im Spiel bereits unter dem Namen "Rundreise" kennengelernt.
 (8) Findest du jeweils alle Hamilton-Kreise in diesen Graphen? Zeichne sie in dein Heft.
(8) Findest du jeweils alle Hamilton-Kreise in diesen Graphen? Zeichne sie in dein Heft.
 Quelle: https://lehrerfortbildung-bw.de/u_matnatech/imp/gym/bp2016/fb1/6_m2_aug/2_kopiervorlagen/3_hamilton/1_uebung/hamilton_ueb1.png
Quelle: https://lehrerfortbildung-bw.de/u_matnatech/imp/gym/bp2016/fb1/6_m2_aug/2_kopiervorlagen/3_hamilton/1_uebung/hamilton_ueb1.png

(9) Graphen in "Auf den Spuren eines Handelsreisenden"
Im Spiel "Auf den Spuren eines Handelsreisenden" habt ihr in jedem Level auf verschiedenen Beispielen von Graphen gespielt. Auf dieser Seite habt ihr erfahren, was die Datenstruktur Graph genau ist, welche Eigenschaften Graphen haben sowie welche Wege auf Graphen gegangen werden können. Beschreibe, welche Elemente von Graphen im Spiel zu finden sind und welche Eigenschaften diese Graphen haben.

(10) Zusatzaufgabe: TSP
Herr Schnell muss Waren ausliefern. Er startet bei seiner Spedition in A, muss dann jede der Städte B,C und D genau einmal anfahren und wieder zur Spedition in A zurückkehren. Die Entfernungen sind in der Tabelle (in km) angegeben.
| A | B | C | D | |
|---|---|---|---|---|
| A | 0 | 98 | 58 | 54 |
| B | 98 | 0 | 56 | 161 |
| C | 58 | 56 | 0 | 125 |
| D | 54 | 161 | 125 | 0 |
- Er möchte auf seiner Tour jeweils in die nächstgelegene, noch nicht besuchte Stadt fahren und am Ende nach A zurückkehren. Gib den Pfad und die Länge seines Weges an. Wie nennt sich der Algorithmus, den Herr Schnell verwendet?
- Zeichne einen gewichteten Graphen. Suche alle Hamiltonkreise und ermittle die kürzeste Route. Wie nennt sich dieser Algorithmus?
Zu einfach? Zusatz-Zusatzaufgabe!
(Quelle: Grund 2018)
Basiert auf: Grund (2018): ZPG-Material IMP. und Magenheim et al. (2009): Informatik macchiato - Cartoon-Informatikkurs für Schüler und Studenten.