Einführung: Graphen
Schiffsverbindungen
Ausgangssituation

(A1)
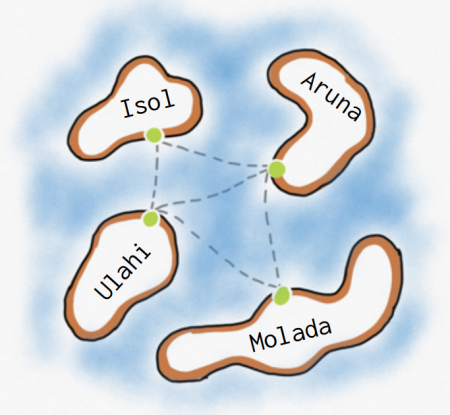
Die Regionalregierung eines Archipels hat eine Fähre angeschafft, die die vier Inseln des Archipels verbinden soll. Dabei sollen die abgebildeten Fährrouten bedient werden. Idealerweise sollte das Schiff immer wieder eine Rundtour fahren, bei der jede Fährverbindung einmal bedient wird.
- Entscheide, ob es eine derartige Rundtour gibt. Gib die Rundtour gegebenenfalls an.
- Entscheide, ob es möglich ist, eine einzige Strecke (≠ Rundtour) zu fahren, bei der jede Route genau einmal bedient wird. Gib an, von welchen Häfen aus dies möglich ist.
- Kannst du angeben, unter welchen Voraussetzungen es eine Rundtour (Starthafen = Zielhafen) gibt, die alle Routen genau einmal abfährt?
Modellierung
Um derartige Fragestellungen in informatischen Systemen modellieren zu können, müssen wir uns nun ein paar Gedanken machen.

(A2)
Welche der folgenden Informationen sind wichtig für die Suche nach Rundtouren:
- Name der Inseln
- Größe der Inseln
- Entfernung zwischen den Häfen
- Welche Inseln sind mit Fährrouten verbunden?
- genauer Verlauf der Fahrtroute
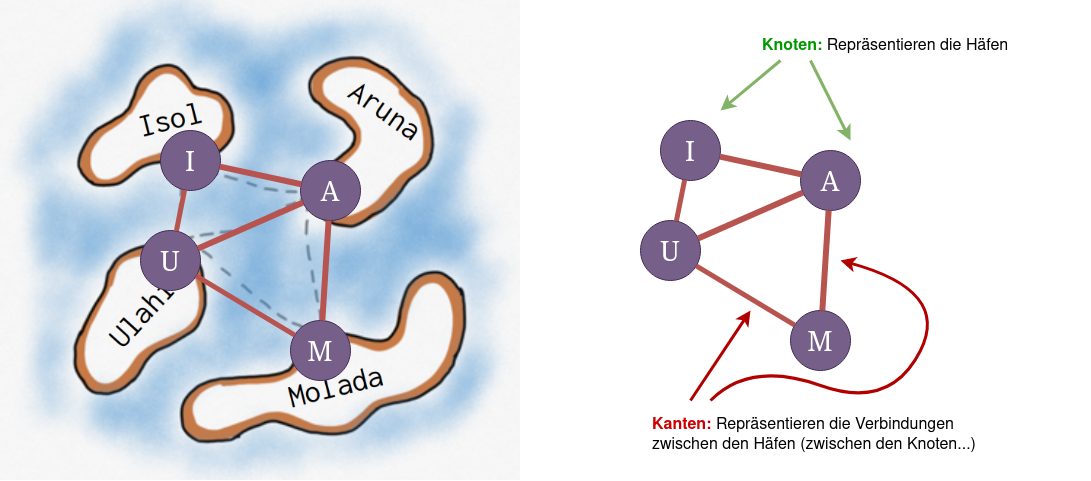
Zur Modellierung kommt also ein Modell zum Einsatz, welches die Häfen und die Verbindungen zwischen den Häfen umfassen muss. Allgemeiner kann man davon sprechen, dass man Knoten modellieren möchte, deren Verbindungen mit Hilfe von Kanten dargestellt werden.
Für unser Archipel sieht das so aus:
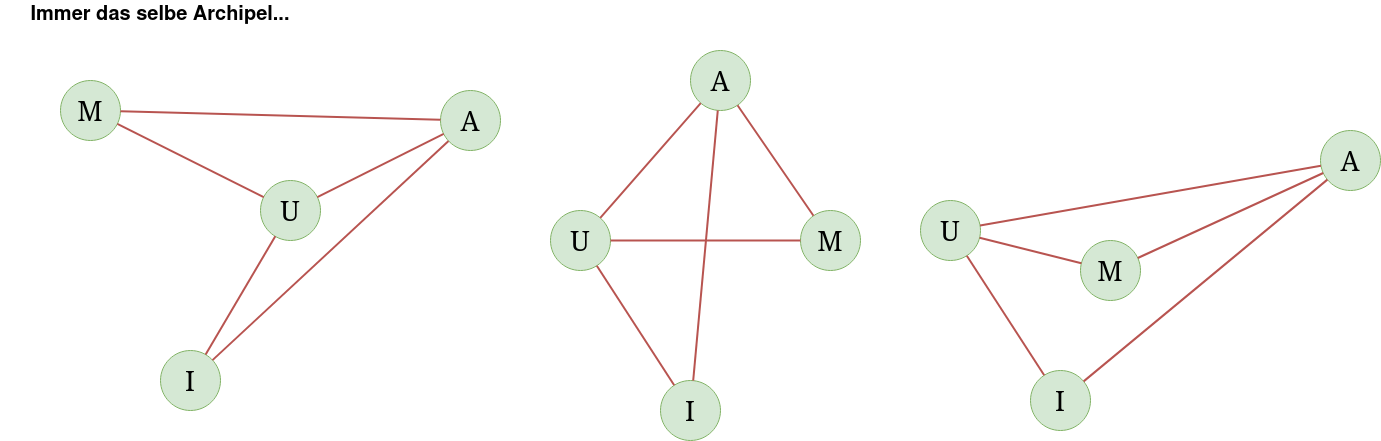
Die Anordnung der Elemente auf der Zeichenfläche spielt dabei überhaupt keine Rolle, solange die Kanten und ihre Verbindungen gleich bleiben, modellieren wir dasselbe Archipel:
Definition: Graph
Ein Graph ist ein Gebilde, das aus Knoten und Kanten besteht. Jede Kante verbindet zwei Knoten oder einen Knoten mit sich selbst. Von einem Knoten können eine, mehrere oder keine Kanten ausgehen.
Formal ist ein Graph also ein 2-Tupel, das aus einer Knotenmenge und einer Kantenmenge besteht und man schreibt:
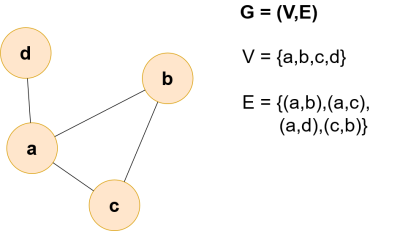
Graph G = (V,E) mit V: Knotenmenge und E: Kantenmenge
Die Buchstaben sind aus den englischen Begriffen abgeleitet: V ist die Menge von Knoten (Vertices) und E die Menge der Kanten (Edges).
Das Bild rechts veranschaulicht die Begriffe, man erkennt dort auch, wie man die Kanten darstellen kann, indem man die verbundenen Knoten in runden Klammern durch ein Komma getrennt angibt. In der Menge der Kanten fehlt (d,b), weil der Knoten d nicht mit dem Knoten b verbunden ist.

(A3)
Zeichne den folgenden Graphen: G=(V,E) mit V = {29,8,1,16,42,3} und E = {(8,42),(8,1),(16,8),(8,29),(1,16),(42,3),(29,42),(3,29)}
Weitere Begriffe
Knotengrad
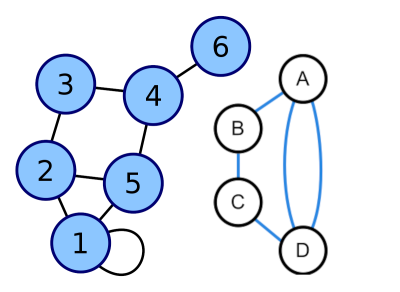
Jeder Knoten hat die Eigenschaft "Grad des Knotens"
Der Grad eines Knotens entspricht der Anzahl der Kantenenden, die mit dem Knoten verbunden sind.1)
grad(C) = 2 grad(A) = 3 grad(4) = 3 grad(1) = 4
Wege in Graphen
- Mit dem Begriff Kantenzug bezeichnen wir einen Pfad durch den Graphen, bei dem Knoten/Kanten auch mehrfach durchlaufen werden dürfen.
- Mit dem Begriff Weg bezeichnen wir einen Pfad durch den Graphen, bei dem jeder Knoten höchstens ein Mal durchlaufen wird.
- Startet ein Kantenzug oder Weg am selben Knoten wie er endet, sind also Start- und Endknoten identisch, bezeichnet man den Kantenzug/der Weg als geschlossen.
- Ein geschlossener Kantenzug heißt Zyklus. Ein Graph, in dem man keinen Zyklus finden kann, heißt zyklenfrei.
- Ein geschlossener Weg heißt Kreis , d.h. Start- und Zielknoten sind gleich und jeder Knoten wird maxmimal ein mal durchlaufen
Zusammenhang
Wenn es in einem Graphen von jedem Knoten zu einem anderen einen Weg gibt, heißt der Graph zusammenhängend.
Einen zusammenhängenden Teilgraphen nennt man Zusammenhangskomponente.
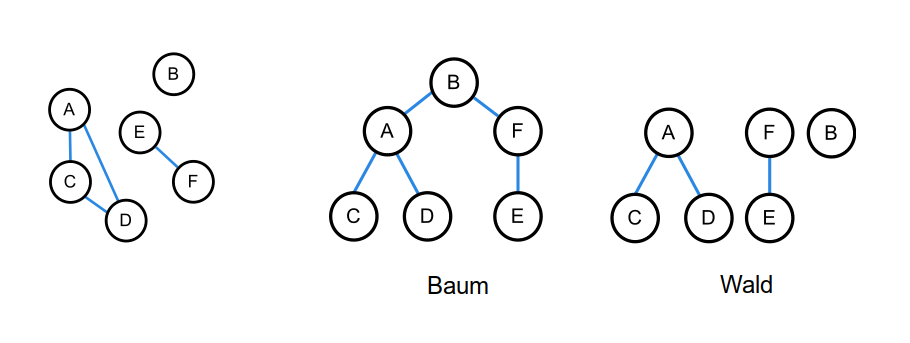
Zusammenhängende, azyklische Graphen sind Bäume.
Eulerzug
Ein Kantenzug, in dem jede Kante genau einmal vorkommt, heißt Eulerzug.
In einem gegebenen Graph gibt es einen Eulerzug wenn
- Der Graph zusammenhängend ist und
- Entweder: Alle Knoten geraden Grad haben oder: genau zwei Knoten ungeraden Grad haben.
Geschlossener Eulerzug
Ein geschlossener Eulerzug (auch Eulerkreis) ist ein Zyklus, in dem jede Kante genau ein mal vorkommt.
Ein Graph besitzt einen geschlossenen Eulerzug, wenn
- Der Graph zusammenhängend ist und
- Alle Knoten geraden Grad haben
Weiterführende Fragen
(A4)
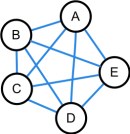
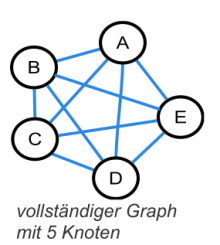
- Zeichne einen vollständigen Graphen mit drei und einen mit vier Knoten.
- Entscheide, ob die Graphen mit drei, vier oder fünf Knoten einen geschlossenen Euler-Zug haben.
- Gib eine allgemeine Regel an, wann ein vollständiger Graph einen geschlossenen Eulerzug hat.
Für viele Anwendungen verwendet man gerichtete Graphen, d.h. die Kanten haben eine Richtung (z.B. bei einem Stadtplan mit Einbahnstraßen). Bei einem Euler-Zug darf man die Kanten dann nur in der vorgegebenen Richtung durchlaufen.
Jeder Knoten hat dann einen Ausgangsgrad (wie viele Kanten gehen von einem Knoten aus) und einen Eingangsgrad (wie viele Kanten führen zu einem Knoten hin).
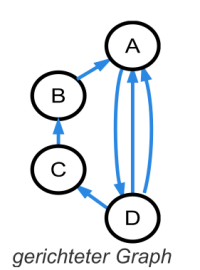

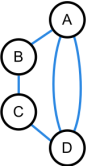
(A5)
- Entscheide, ob der abgebildete Graph einen geschlossenen Euler-Zug hat.
- Gib eine allgemeine Regel an, wann ein gerichteter Graph einen geschlossenen Euler-Zug hat.