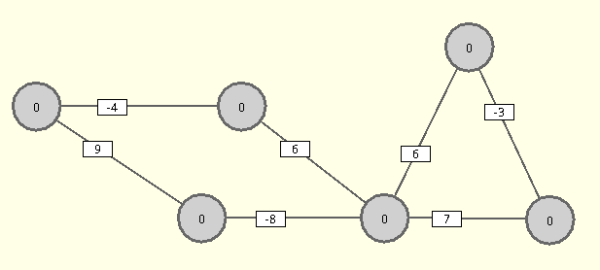
Der Bellman-Ford Algorithmus
Der Bellman-Ford-Algorithmus berechnet die Kosten der günstigsten Wege von einem Startknoten aus zu allen anderen Knoten im Graph. Auf diese Weise kann er also auch die günstigsten Wege selbst konstruieren. Anders als der Dijkstra Algorithmus kann der Bellmann-Ford Algorithmus auch mit negativen Kantengewichten rechnen.
Der Algorithmus geht iterativ vor, er geht also zunächst von einer schlechten Schätzung der Kosten aus, und verbessert diese so lange, bis die korrekten Werte gefunden sind.
Die erste Schätzung ist:
- Der Startknoten hat Kosten 0, denn seine Entfernung zu sich selbst ist natürlich 0.
- Alle anderen Knoten haben Kosten "unendlich" - schlechter geht es also nicht.
Anschließend werden alle Kanten auf folgende Bedingung geprüft: Ist der Wert des Anfangsknotens der Kante plus die Kosten für die Benutzung der Kante niedriger als der Wert des Zielknotens der Kante?
Wenn das der Fall ist, haben wir eine Abkürzung gefunden: Es ist besser, die eben geprüfte Kante zu nutzen, als den bisherigen Weg. Der Wert des Zielknotens der Kante wird entsprechend aktualisiert: Sie entsprechen jetzt genau den Kosten des Anfangsknotens der Kante plus den Kosten für die Benutzung der Kante.
- Alle Kanten des Graphen zu betrachten und die Kosten der Knoten zu aktualisieren, nennt man eine Phase des Algorithmus.
- Es reicht es nicht aus, alle Kanten nur einmal zu betrachten. Nach der ersten Phase wurden die Kosten für alle Knoten korrekt berechnet, für die der günstigste Weg nur eine Kante beinhaltet. Nach 2 Phasen haben wir schon die Wege, die maximal 2 Kanten benutzen, korrekt berechnet und so weiter.

(A1)
Wieviele Phasen müssen maximal durchlaufen werden, um einen Graphen mit n Knoten sicher vollständig zu untersuchen?

(A2)
- Notiere anhand der Beschreibung oben eine erste Version des Algorithmus als Pseudocode.
- Implementiere deinen Pseudocode im Graphentester.

(A3)
Welche Situation muss vermieden werden, damit die Zulässigkeit von negativen Kantengewichten nicht zu unsinnigen Ergebnissen führt?
Wie kann man das im Algorithmus prüfen?