Traversierungen

Eine der wichtigsten Operationen auf einem Graphen ist die Traversierung. der Begriff Traversierung bedeutet dabei, dass der Graph beginnend von einem Startknoten entlang der vorhandenen Kanten durchlaufen wird. Bei gerichteten Graphen wird dabei auch die Kantenrichtung berücksichtigt.

Die beiden grundlegenden Traversierungsarten sind die Tiefensuche und die Breitensuche.¹⁾

Bei der Breitensuche werden die Knoten eines Graphen "in Ebenen" untersucht, und zwar in der Reihenfolge der zunehmenden Entfernung vom Startknoten.

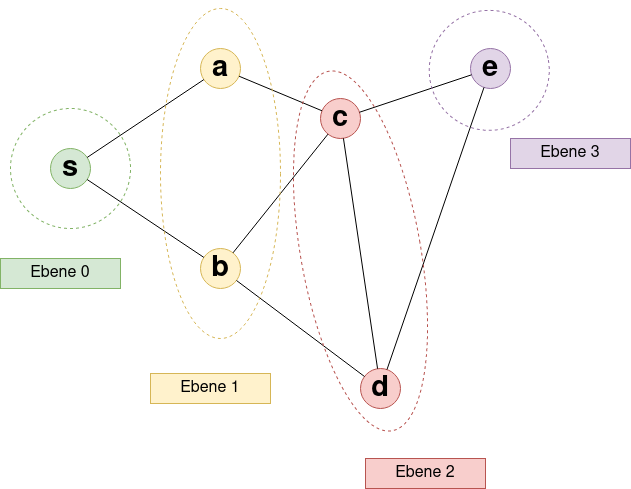
Ebene 0 enthält den Startknoten s, sonst nichts. Ebene 1 ist die Menge der Knoten, die eine Kante von s entfernt sind, also die Nachbarn von s. Diese Knoten werden bei der Breitensuche direkt im Anschluss des Startknotens untersucht, die Nachbarknoten dieser Knoten werden zur Untersuchung in Ebene 2 vorgemerkt.

Im Beispielgraph sind a und b die Nachbarn des Startknotens s und bilden somit die Ebene 1.

Allgemein sind die Knoten, die in der Eben i verarbeitet werden, diejenigen die zu einem Knoten in Schicht i-1 benachbart sind und nicht bereits zu einer der Schichten 0, 1, 2, …, i-1 gehören.

Die Breitensuche bearbeitet alle Knoten der nächsten Ebene i unmittelbar nach Abschluss der Erkundung von Ebene i-1

Zulässige Abfolgen für eine Breitensuche im Beispielgraphen wären also z.B. s,a,b,d,c,e oder auch s,b,a,c,d,e.

Implementiert wird die Breitensuche mit Hilfe einer Queue für die unbearbeiteten Knoten. Eine Schlange oder eine Queue ist eine einfach "First-In-First-Out"-Datenstruktur, der Pseudocode für eine Breitensuche sieht folgendermaßen aus:

// Breitensuche
markiere den Startknoten s als markiert, alle anderen Knoten als nicht markiert
Q := Ist eine Schlange, die mit dem Startknoten s initialisisert wird

solange "Q ist nicht leer":
  Entferne den ersten Knoten v der Schlange Q
  für alle Nachbarn w von v:
    wenn w nicht markiert ist:
      setze w als markiert
      füge w ans Ende der Schlange Q an
    ende_wenn
  ende_für
ende_solange

Die folgende Grafik zeigt den Ablauf am Beispielgraphen von oben. Rechts ist jeweils der Zustand des Queues dargestellt, gestrichelt ist dargestellt, wie sich die "Ebenengrenze" verschiebt. Neue Knoten werden links in den Queue eingestellt und rechts entnommen/gelöscht.

Bei der Tiefensuche werden die Knoten des Graphen nicht wie bei der Breitensuche "vorsichtig" Ebene für Ebene besucht, sondern es werden ausgehend vom aktuellen Knoten immer zuerst die gefundenen Nachbarknoten besucht. Realisiert wird das in der iterativen Variante des Algorithmus durch einen Stack für die zu besuchenden Knoten.

// Breitensuche
markiere den Startknoten s als markiert, alle anderen Knoten als nicht markiert
S := Ist ein Stapel, der mit dem Startknoten s initialisisert wird

solange "S ist nicht leer":
  Entferne den obersten Knoten v vom Stack S
  für alle Nachbarn w von v:
    wenn w nicht markiert ist:
      setze w als markiert
      lege w auf dem Stack S ab
    ende_wenn
  ende_für
ende_solange

Die folgende Abbildung zeigt den Ablauf:

Man kann gut erkennen, dass der Graph zunächst in der "Tiefe" bis zum Knoten e durchlaufen wird, bevor es beim Nachbarn b des Startknotens weitergeht.

Implementiere Breiten- und Tiefensuche im Graphentester in einem eigenen Algorithmus. Färbe die besuchten Knoten ein und nummeriere sie, sodass du den Ablauf nachvollziehen kannst. Teste deine Algorithmen mit dem Beispielgraphen 03_routenplanung/00_traversierung.

Für den Queue kannst du z.B. das Queue-Interface mit einer Linked-List verwenden:

import java.util.LinkedList;
import java.util.Queue;
 
Queue<Knoten> q = new LinkedList<>();
q.add(s);  // Fügt den Knoten der Queue am Ende hinzu s, muss ein Knoten sein
Knoten aktuell = q.remove(); // Entfernt den vordersten Knoten aus der Queue
Knoten vorne = q.peek();  // Gibt den vordersten Knoten zurück, ohne ihn zu entfernen
int size = q.size() // Gibt die Zahl der Elemente in der Schlange zurück
// q.isEmpty() ist wahr, wenn die Schlange leer ist.

Für den Stack kannst du die Klasse Stack verwenden:

import java.util.Stack
 
Stack<Knoten> st = new Stack<>();
st.push(k) // Legt den Knoten k auf den Stapel
Knoten aktuell = st.pop() // Hebt den obersten Knoten ab
st.isEmpty() // ist wahr, wenn der Stapel leer ist

Hilfe Grafentester