Einstieg: Modellierung mit Graphen
Situation 1
Modelliert werden sollen die Beziehung zwischen Personen, in diesem Beispiel festgelegt durch den Umstand, ob eine Person die Handynummer einer anderen Person kennt. In der Liste sieht man, wer welche Nummern gespeichert hat.
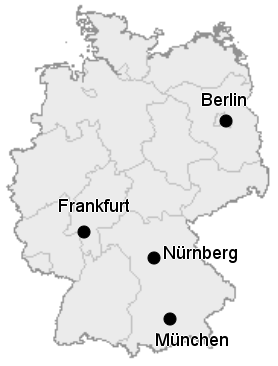
Situation 2 (Traveling Salesman Problem)
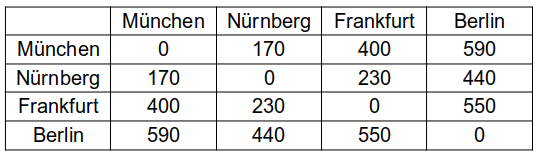
Ein Geschäftsmann aus Frankfurt muss Kunden in Berlin, Nürnberg und München beraten. Er möchte seine Rundreise so planen, dass er jeden Ort nur genau einmal besucht und die Gesamtfahrstrecke dabei möglichst klein bleibt. Dazu hat er die Entfernungen (in km) in einer Tabelle aufgeschrieben:
Aufgaben

(A1)
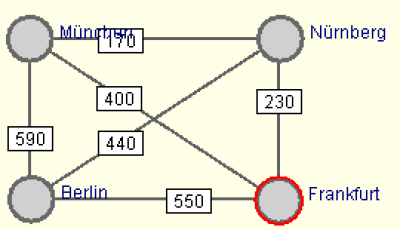
Beide Situationen sollen als Graph modelliert werden.
- Entscheide für beide Situationen, ob es sich um einen gerichteten oder ungerichteten Graphen handelt.
- Entscheide für beiden Situationen, ob es sich um einen gewichteten oder einen ungewichteten Graphen handelt.

(A2)
Zeichne die Graphen für beide Situationen.
Begriffe
Graphen können auf zwei Arten so dargestellt werden, dass sie von Rechnersystemen effizient verarbeitet werden können.
- Als Adjazenzliste
- Als Adjazenzmatrix
Adjazenz bedeutet in diesem Zusammenhang "Nachbarschaft".
Wenn zwei Knoten über eine Kante miteinander verbunden sind, heißen diese Nachbarknoten, sie sind benachbart oder auch "adjazent".
Erarbeitung
 (3A) Gruppe A: Bearbeite bitte diese Seite: Adjazenzmatrix
(3A) Gruppe A: Bearbeite bitte diese Seite: Adjazenzmatrix
 (3B) Gruppe B:Bearbeite bitte diese Seite: Adjazenzliste
(3B) Gruppe B:Bearbeite bitte diese Seite: Adjazenzliste