AES etwas genauer betrachtet
Um diesen Abschnitt bearbeiten zu können, solltest du mit den wesentlichen Begriffen der modernen symmetrischen Kryptoverfahren vertraut sein.
Schlüssellänge und Rundenzahl
Die Blocklänge des AES beträgt 128 Bit. Die AES-Schlüssellänge kann wahlweise auf 128, 192 oder 256 Bit festgelegt werden, die Rundenzahl hängt von der gewählten Schlüssellänge ab:
| Schlüssellänge | Rundenzahl |
|---|---|
| 128 Bit | 10 |
| 192 Bit | 12 |
| 256 Bit | 14 |
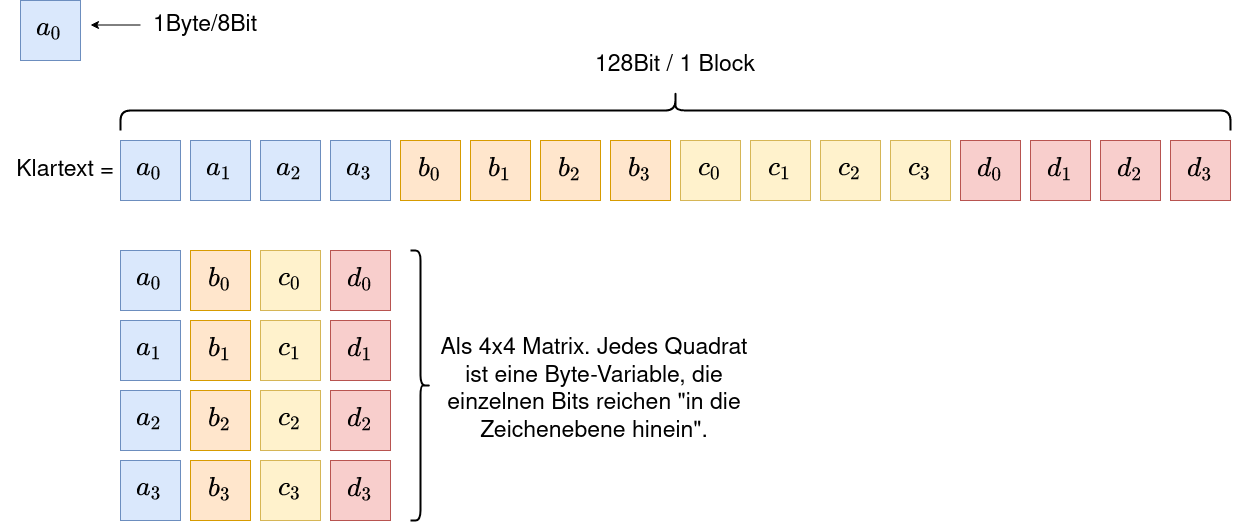
Klartextblock als Matrix
Alle Operationen werden auf einer 4x4 Byte Matrix ausgeführt, dazu werden die 128Bit des Klartextblocks wie folgt angeordnet:
Rundenaufbau
Wir betrachten nur den AES mit 128Bit Schlüssellänge und 10 Runden.
Der AES verfügt über die folgenden Operationen, die im Ablauf der Runden zum Einsatz kommen und auf der 4x4 Byte Matrix ausgeführt werden:
- SubBytes
- ShiftRow
- MixColumn
- AddRoundKey
Die mathematischen Details der Operationen beleuchten wir an dieser Stelle nicht.
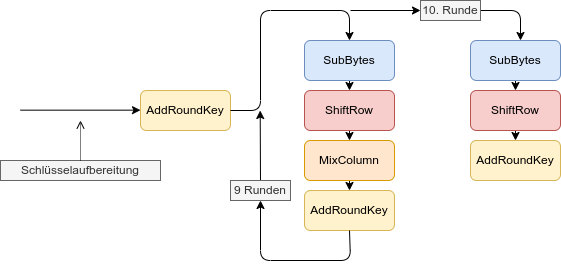
Der Ablauf ist wie folgt:

(A1)
Wieviele Rundenschlüssel sind nötig? Wie viel (Bit/Byte) Schlüsselmaterial muss bei der Schlüsselaufbereitung erzeugt werden? Ein Rundenschlüssel ist 16Byte lang.
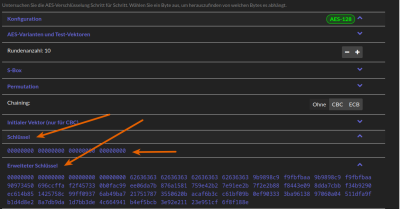
Beobachte die Schlüsselaufbereitung im Cryptool. Klappe die Abschnitte Schlüssel und Erweiterter Schlüssel aus. Ändere anschließend den Wert für den Schlüssel und beobachte, was im Feld erweiterter Schlüssel geschieht.
Überprüfe, ob die Menge des Schlüsselmaterials beim erweiterten Schlüssel mit deinen eigenen Überlegen übereinstimmt.
Was macht SubBytes?
Die Rundenfunktion "SubBytes" dient zur kryptographischen Konfusion und ist mit einer S-Box realisiert. Die AES S-Box ist eine feste Zuordnungstabelle, in der für jeden Byte-Wert von 00 bis FF (0-255) festgelegt ist, durch welchen anderen Byte-Wert ein Eingabebyte ersetzt werden soll.
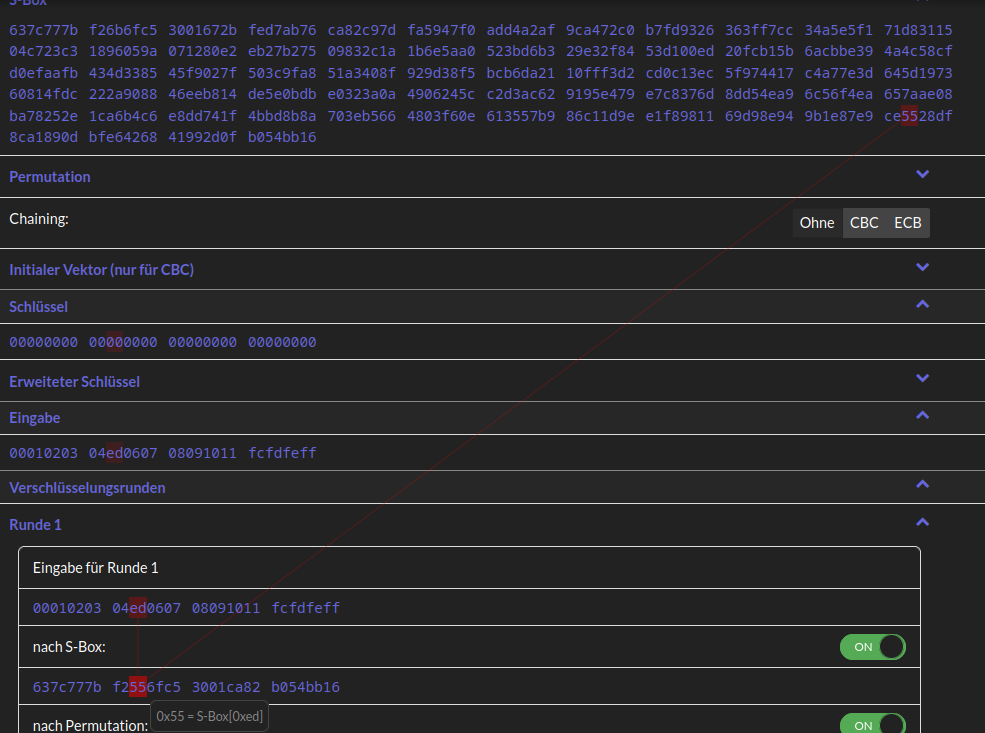
Bei der Ersetzung wird nun jedes Byte der 4x4 Matrix durch seine entsprechende Ersetzung ersetzt. Im Cryptool kann man die AES S-Box sehen:
Dabei sind 2 Hexadezimale Stellen jeweils ein Byte und man zählt vom Beginn der S-Box an von 00 bis FF (von 0 bis 255), damit ergeben sich folgende Ersetzungen:
00 -> 63 01 -> 7c 02 -> 77 ... fe -> bb ff -> 16

(A2)
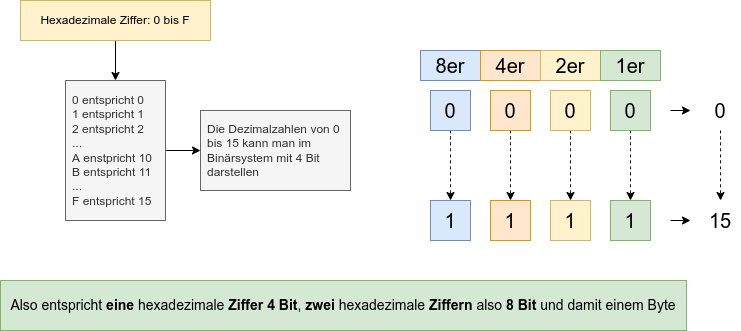
Mache dir zunächst noch einmal klar, dass 2 hexadezimale Ziffern 8 Bit, also ein Byte repräsentieren.
Arbeite im Cryptool zunächst mit dem Schlüssel 00000000 00000000 00000000 00000000 und der Eingabe 00010203 04050607 08091011 fcfdfeff.
Das hat zur Folge, dass die erste Anwendung von AddRoundKey auf den Eingabetext - bevor die Runden beginnen - keine Auswirkung auf die Bitfolge hat, auf die die S-Box angewandt wird.
Mache dir klar, dass die Eingabe von 0 beginnend hoch zählt (12Bytes weit), beziehungsweise von 255 beginnend abwärts zählt (4Bytes weit).
Tipp: Wenn du im Cryptool die Bytes der Ergebnisse der Rundenoperationen anklickst, veranschaulicht Cryptool durch dünne Linien, wie der Byte-Wert zustandekommt.
- Vollziehe die Funktionsweise der S-Box an diesem Beispiel nach, indem du die Ersetzungen der ersten 12 sowie der letzten 4 Bytes im Feld
nach S-Box:des Cryptool überprüfst. - Ändere den Eingabetext und beobachte die Auswirkungen. Findest du passende Ersetzungen?
- Ändere den Schlüssel und beobachte die Auswirkungen: Warum ändert sich jetzt die Bitfolge für das Feld
Eingabe für Runde 1?
Zusatzfrage: Welcher Text ist in der folgenden Eingabe codiert? 496e666f 20697374 20746f6c 6c21210a
Die Funktionsweise von ShiftRow
ShiftRow dient zur kryptographischen Diffusion. Im Cryptool wird "ShiftRow" als Permutation (Vertauschung) benannt.
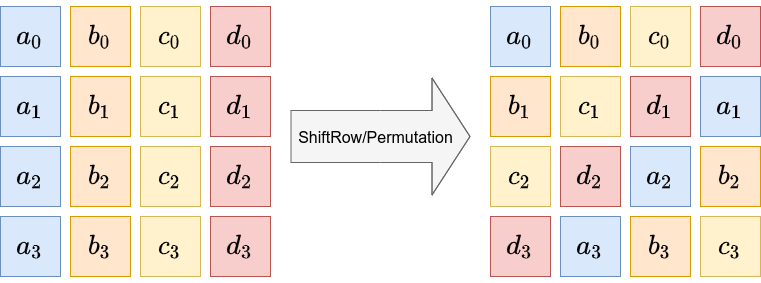
Anschaulich rotiert ShiftRow die Bytes in den Zeilen der 4x4 Matrix des Byte-Blocks:
Im Cryptool ist die Permutation durch eine entsprechende Bytefolge im Abschnitt Konfiguration festgelegt. Für den "Standard AES" Algorithmus wird stets getauscht, wie im Bild dargestellt.

(A3)
Vollziehe im Cryptool nach, dass die Bytes in den Zeilen tatsächlich so vertauscht werden, wie im Bild oben dargestellt.
- Wie gelangt man von der Darstellung im Cryptool (z.B.:
637c777b f2556fc5 3001ca82 b054bb16zur Matrix wie im Bild dargestellt? - Notiere die Matrix für ein Beispiel aus Cryptool einmal vor und einmal nach ShiftRow.
MixColumn
Die Funktion MixColumn trägt wie ShiftRow zur Diffusion bei. Im Vergleich zum sehr simplen ShiftRow ist MixColumn komplexer, es wird eine spezielle "Multiplikation" der Bytes in der Matrix verwendet, welche mit "Exklusiv-Oder" Verknüpfungen kombiniert wird. Eine genaue Betrachtung führt an dieser Stelle zu weit.
Wichtig: Während ShiftRow für eine Durchmischung der Zeilen sorgt, führt MixColumn ein spaltenweises Mischen durch.

(A4)
Vollziehe im Cryptool nach, dass MixColumns tatsächlich aus allen Bytes einer Spalte ein neues Element der Byte-Matrix erzeugt und damit tatsächlich die Spalten durchmischt.
AddRoundKey
Die Funktion AddRoundKey verknüpft die Eingabe einer Runde exklusiv oder mit dem Rundenschlüssel. Vor der ersten Runde wird AddRoundKey mit dem ursprüngliche AES Schlüssel auf diese Weise mit dem Eingabetext verknüpft.

(A5)
Vollziehe die erste Verknüpfung des AES Schlüssels mit dem Klartext im Cryptool nach.
- Verwende dazu zunächst als Schlüssel
00000000 00000000 00000000 00000000. Der Eingabetext wird durch das initiale AddRoundKey nicht verändert - warum nicht? - Ändere nun den Schlüssel an einer Stelle (z.B. ganz am Ende) und beobachte die Änderung des Felds
Eingabe für Runde 1. Vollziehe diese Veränderung mit der XOR Verknüpfung nach. Dazu kannst du die betroffenen Bytes Bitweise untereinander schreiben.1)
Vollständiger Verschlüsselungsvorgang
Jetzt können wir einen gesamten Verschlüsselungsvorgang nachvollziehen.

(A6)
Vollziehe eine vollständige Verschlüsselung über alle 10 Runden grob nach:
- Mache dir klar, dass das Ergebnis einer Runde stets als Eingabe der folgenden Runde verwendet wird.
- Beobachte die Verwendung der 11 Subkeys im Verlauf der Verschlüsselung - wird tatsächlich in jeder Runde ein anderen Rundenschlüssel verwendet?
- Untersuche, ob in Runde 10 MixColumn durchgeführt wird oder nicht.
- Mache dir klar, dass durch diesen Ablauf ein Block von 128Bit Daten (Klartext) auf einen Block von 128Bit Daten "abgebildet" werden, die nun als Geheimtext bezeichnet werden können. Das geschieht in 10 Runden - beim AES handelt es sich also um eine rundenbasierte Blockchiffre.
Zusatzaufgabe: Entschlüsselung
- Vollziehe die Entschlüsselung nach.
- Erstelle ein Ablaufdiagramm wie oben für den Entschlüsselungsvorgang.