Hashfunktionen
Ein kleines soziales Netz
Passwörter speichern
Für eine Microblogging Plattform möchtest du die Zugangsdaten deiner Nutzer in der einer Datenbank speichern, insbesondere den Benutzernamen und das Passwort, das die Benutzer zur Anmeldung verwenden. Weil du in Informatik gut aufgepasst hast, ist dir sofort klar, dass es nicht in Frage kommt, die Passwörter unverschlüsselt in der Datenbank abzulegen.
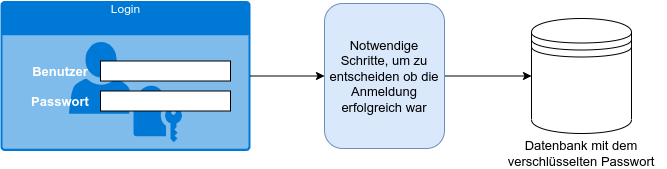
Dein erster Gedanke ist: Die speichere ich verschlüsselt in der Datenbank ab! Die Situation stellt sich also wie folgt dar:

(A1)
Fritz Mayer meldet sich durch Eingabe seines Benutzernamens und seines Klartextpassworts am Login Formular an.
- Überlege dir, wie der Vorgang ablaufen könnte, der dazu führt, den Anmeldeversuch bei Eingabe des richtigen Passworts als "korrekt" zu bewerten.
- Welche Probleme erkennst du, wenn das Passwort verschlüsselt in der Datenbank gespeichert wird?
Die Prüfsummenstrategie
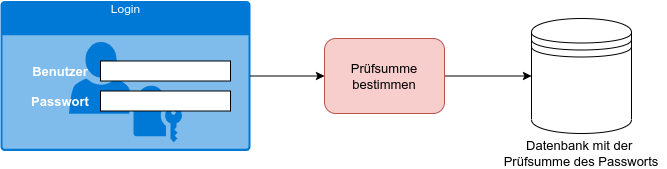
Du überlegst dir, anstatt des verschlüsselten Passworts eine Prüfsumme in der Datenbank zu hinterlegen. Jetzt kannst du die Prüfsumme eines eingegebenen Passworts berechnen und mit der gespeicherten Prüfsumme vergleichen:
Dein Entwicklungschef schlägt dir zwei Möglichkeiten vor:
- Die iterierte Quersumme ist die Quersumme, die entsteht, wenn man solange immer wieder die Quersumme ausrechnet, bis nur noch eine einzige Ziffer übrig bleibt. Beispiel: Für die Zahl 97 lautet die normale Quersumme 16, berechnet man davon wiederum die Quersumme, so entsteht die iterierte Quersumme: 7.
- Die alternierende Quersumme entsteht durch abwechselndes Subtrahieren und Addieren der einzelnen Ziffern. Beispiel: Für die Zahl 1234 ist die alternierende Quersumme 1 - 2 + 3 - 4 = -2).
Um unsere Überlegungen einfach zu halten, lassen wir fürs Erste nur Kennwörter zu, die aus Zahlen bestehen.
| Benutzername | Passwort | Iterierte QS | Alternierende QS |
|---|---|---|---|
| martin | 12345 | 1+2+3+4+5 = 15 → 1+5 = 6 | 1-2+3-4+5 = 3 |
| susi | 123456 | ||
| franzi | 12223345678 | ||
| karle | 123456789 | ||
| eva | 1234567890 | ||
| kathrin | 11111121 | ||
| hubertus | 191817 |

(A2)
- Ergänze die Tabelle für die weiteren Zeilen.
- Entscheide für welche Methode der Passwortspeicherung du dich entscheiden würdest. Begründe deine Entscheidung.
- Welche Eigenschaft würdest du dir von einer optimalen Prüfsumme wünschen? Erläutere, warum diese auf deiner Wunschliste stehen würde.
Bessere "Prüfsummen"-Methoden
Deine Entwickler stimmen dir zu, dass das so keinen Sinn macht und schlagen weitere Prüfsummen vor:
| Benutzername | Passwort | Methode 1 | Methode 2 | Methode 3 |
|---|---|---|---|---|
| martin | 12345 | 54321 | 34567 | 120 |
| susi | 123456 | 654321 | 345678 | 720 |
| franzi | 1222334567 | 7654332221 | 3444556789 | 60480 |
| karle | 4534567 | 7654354 | 6756789 | 50400 |
| eva | 657703 | 307756 | 879923 | 4410 |
| kathrin | 11111121 | 12111111 | 33333343 | 2 |
| hubertus | 191817 | 718191 | 31131039 | 504 |

(A3)
- Finde heraus, welche Methoden zur "Prüfsummenbildung" hier zum Einsatz kommen.
- Wenn du dich für eine dieser drei Methoden entscheiden müsstest - welche wäre dies? Begründe deine Wahl.
Hashfunktionen
In der Kryptographie spielen sogenannte Hashfunktionen eine große Rolle (wie wir bei genauerer Betrachtung noch sehen werde…)
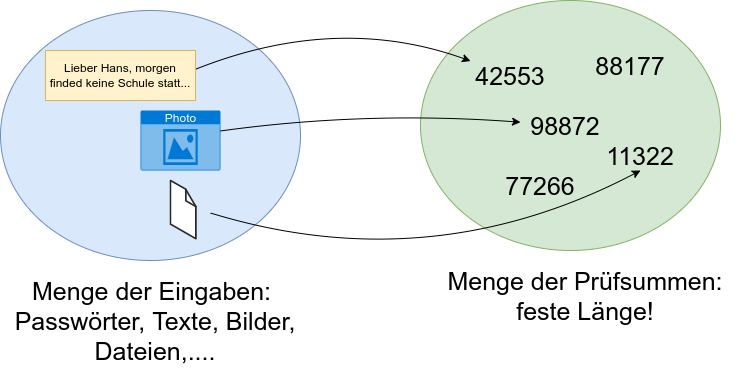
Diese Hashfunktionen sind unseren "Prüfsummen" nicht unähnlich, haben aber noch eine erschwerende Randbedingung zu erfüllen: Es sollen beliebig große Eingaben auf eine feste Zahl von Zeichen abgebildet werden:

(A4)
Überlege dir, welche Auswirkungen diese "Randbedingung" auf unsere beiden Wünsche an die "Prüfsummenfunktion" haben:
- Wunsch 1: Unsere Prüfsumme soll kollisionsfrei sein.
- Wunsch 2: Unsere Prüfsumme soll unumkehrbar sein.
Kryptographische Hashfunktionen:
- … bilden eine beliebig große Eingabemenge auf Hashes fester Länge ab. Meist erfolgt die Ausgabe Hexadezimal.
- … sind nicht umkehrbar
- … sind kollisionsarm. Insbesondere soll es unmöglich sein Kollisionen zu konstruieren, also Eingaben finden zu können, die denselben Hash Wert haben
Beispiele:
- MD5 (gebrochen – man kann Kollisionen konstruieren)
- SHA1 (unsicher, kommt derzeit bei GIT zum Einsatz)
- SHA2 (mehrere Varanten, gilt als weitgehend sicher)
- Bcrypt (wird zum Passworthashing verwendet)

(A5)
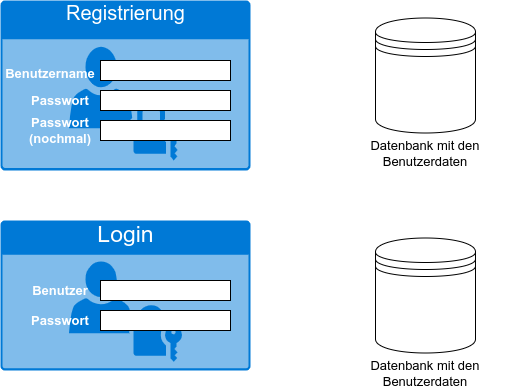
Beschreibe stichwortartig, was bei der Registrierung eines neuen Benutzers an deinem sozialen Netzwerk geschehen muss, um den neuen Benutzer in der Datenbank einzutragen. Was gibt der Benutzer ein, was macht das Softwaresystem, was wird in die Datenbank eingetragen?
Verfahre ebenso beim Anmeldevorgang eine bestehenden Benutzers: Was gibt der Benutzer ein, was macht das Softwaresystem, was wird aus der Datenbank gelesen?
Praktische Aufgaben
Unter Linux gibt es mehrere Kommandozeilenwerkzeuge, mit Hilfe derer man kryptographische Hashes bestimmen kann. Bearbeite die folgenden Aufgaben auf der Kommandozeile. Halte deine Ergebnisse in deinen Notizen fest.

(P1)
Bestimme den Hashwert des Wortes "Hallo" indem du die Ausgabe des echo-Befehls an einen entsprechenden Hash-Befehl weiterleitest:
echo "Hallo" | md5sum echo "Hallo" | sha1sum echo "Hallo" | sha224sum
- Gib für jeden Hash-Befehl die Länge des Hashs in Bit an.
Vergleiche die Ausgabe der beiden folgenden Befehle:
echo "Hallo" | md5sum echo -n "Hallo" | md5sum
- Was fällt auf, wenn man die Hash-Werte vergleicht? Woran liegt das? Die Manual-Page für den echo-Befehl kann dir weiterhelfen (
man echo).

(P2)
Man kann auch Hash-Werte für ganze Dateien bestimmen:
sha1sum <Dateiname>
z.B.:
sha1sum mail.txt 6ce3fe1479a10edb2f1bdd6d181a5b0e210abe1a mail.txt
- Erstelle eine Datei mit dem Namen
mail.txt, schreibe einige Worte hinein. - Bestime den SHA1-Hash der Datei
- Ändere ein Zeichen in der Datei, beispielsweise einen Punkt und bestimme erneut den SHA-Hash.
- Bestimme weitere Hash-Werte von Dateien, auch von Bildern, zip-Archiven oder anderen binären Dateiformaten.

(P3)
Kannst du mit den gewonnenen Erkenntnissen ein Verfahren "erfinden", bei dem kryptografische Hashfunktionen bei der Signatur unverschlüsselter Mails zum Einsatz kommen könnten? Du kannst dich hinsichtlich der folgenden Fragestellungen auch im Netz informieren:
- Wie kann man mit Hilfe des RSA-Verfahrens Informationen signieren?
- Wie kann eine Hashfunktion hier hilfreich sein?
Material
| Filename | Filesize | Last modified |
|---|---|---|
| abschlussaufgabe.drawio.png | 34.8 KiB | 23.02.2022 18:43 |
| anmeldung.drawio.png | 26.9 KiB | 23.02.2022 15:58 |
| hash.drawio.png | 62.7 KiB | 23.02.2022 17:57 |
| hashes.odp | 292.7 KiB | 23.02.2022 18:46 |
| hashes.pdf | 216.7 KiB | 23.02.2022 18:46 |
| pruefsumme.drawio.png | 20.4 KiB | 23.02.2022 16:05 |