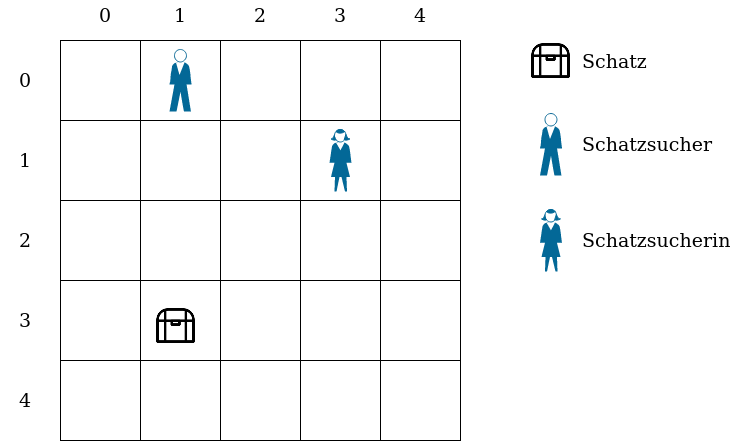
Schatzssuche
Im Folgenden sollen Teile eines Spiels implementiert werden, in dem zwei Schatzsucher auf einem quadratischen Spielfeld, hier als „Welt“ bezeichnet, einen Schatz suchen. Die genauen Spielregeln für die Schatzsuche selbst sind für die folgenden Aufgaben nicht relevant, es geht lediglich darum, die Welt mit einem Schatz und den Suchern anzulegen und zu verwalten.
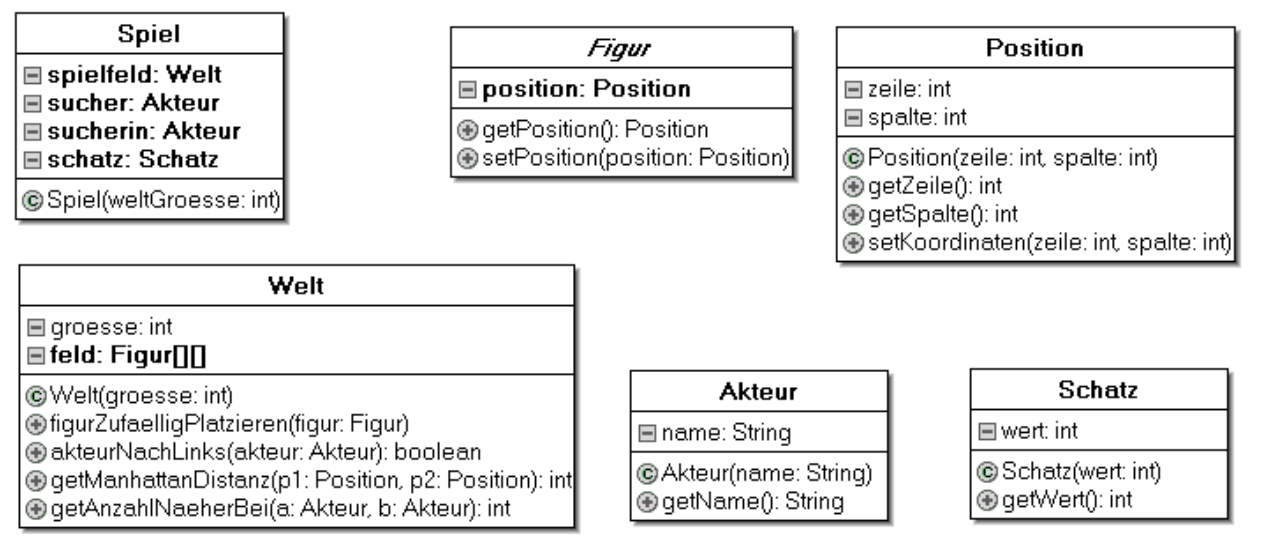
In der Implementierung besitzt die Klasse Welt ein zweidimensionales Array zur Speicherung
des Spielfeldes. Das Attribut groesse gibt die Länge und Breite des Arrays an. Jedes Element
des Arrays entspricht einem Feld der Welt. Der Eintrag null im Array steht für ein
leeres Feld, andernfalls kann mit feld[i][j] die Figur in der i-ten Zeile und j-ten Spalte angesprochen werden. Eine Figur kann entweder ein Akteur oder ein Schatz sein.
Teil 1

(T1A1)
Übertrage die UML-Klassendiagramme – ohne die Attribute und die Methoden – auf dein Lösungsblatt und ergänze die Klassenbeziehungen, indem du die gerichteten Assoziationen und Vererbungen einzeichnest.
Anmerkung: Für die folgenden Programmieraufgaben dürfen Methoden, die im obigen UML-Klassendigramm aufgeführt sind, auch benutzt werden, sofern in der konkreten Aufgabenstellung nichts anderes gefordert wird. Die Programmieraufgaben sind – als Übung für die Abiturprüfung – auf Papier zu lösen.

(T1A2)
Implementiere die Klasse Position aus dem UML-Klassendiagramm.

(T1A3)
Implementieren Sie einen Konstruktor Spiel(weltGroesse: int) so, dass eine
Welt der Größe weltGroesse mit zwei Schatzsuchern namens "Anton" und "Berta"
und einem Schatz im Wert von 50EUR erzeugt wird. Die Schatzsucher und der Schatz
sollen unter Verwendung der Methode figurZufaelligPlatzieren(figur: Figur)
aus der Klasse Welt eine zufällige Startposition erhalten.
Hinweis: Sie dürfen davon ausgehen, dass die Methode figurZufaelligPlatzieren bereits implementiert ist.

(T1A4)
Implementiere Methode akteurNachLinks(akteur: Akteur): boolean
der Klasse Welt so, dass ein Akteur in der Welt um ein Feld nach links verschoben
wird, falls das entsprechend der Grenzen der Welt möglich ist und das Zielfeld nicht
bereits von einer anderen Figur besetzt ist.
Die Methode soll true zurückgeben, falls die Verschiebung erfolgreich war, andernfalls false.
Die Information, wo sich eine Figur in der Welt befindet, ist an zwei Stellen gespeichert: Einerseits im Attribut position in der Klasse Figur, andererseits indirekt im Array feld der Klasse Welt.

(T1A5)
Beschreibe wie die Methode akteurNachLinks jeweils abgeändert werden müsste, wenn man auf das Attribut position in der Klasse Figur bzw. das Array feld in der Klasse Welt verzichten würde.
Teil 2

(T2A1)
Die Methode getManhattanDistanz(p1: Position, p2: Position): int
in der Klasse Welt gibt das Ergebnis von abs(p1.getZeile()-p2.getZeile())
+ abs(p1.getSpalte()-p2.getSpalte()) zurück.
Dabei berechnet die Methode abs den aus der Mathematik bekannten Betrag.
- Begründe, dass die Methode
getManhattanDistanzdie Anzahl der Schritte angibt, die mindestens nötig sind, um von Positionp1zu Positionp2zu gelangen, wenn nur waagerechte und senkrechte Bewegungen erlaubt sind. - Implementiere die Methode
getAnzahlNaeherbei(a: Akteur, b: Akteur): intin der Klasse Welt,
die die Anzahl der Felder zurückgibt, die näher bezüglich der Manhattan-Distanz bei Akteur a als bei Akteur b liegen.
Teil 3
 Das Schatzsuchespiel soll um eine Highscore-Liste erweitert werden. Dazu wird eine Klasse
Das Schatzsuchespiel soll um eine Highscore-Liste erweitert werden. Dazu wird eine Klasse Spieler
eingeführt mit den Attributen name und punkte. In der Klasse Spiel wird zusätzlich noch eine
spielerListe in Form eines Arrays verwaltet.
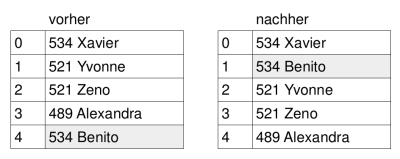
Nach dem Abschluss eines Spiels wird der neue Spieler an das Ende der bereits absteigend sortierten Highscore-Liste angehängt. Dann wird die Liste neu sortiert.
Bei Punktegleichstand soll derjenige Spieler weiter vorne in der Liste stehen, der diesen Punktstand zuerst erreicht hat. Sortierverfahren, die dies gewährleisten, nennt man stabil.

(T3A1)
Für das Sortieren werden zwei Algorithmen vorgeschlagen
Algorithmus I
for i = 0 ... spielerAnzahl-1
for j = 1 ... spielerAnzahl-1
if (spielerListe[j-1].getPunkte() < spielerListe[j].getPunkte()) then
tausche Spieler j mit Spieler (j-1) in spielerListe
endif
endfor
endfor
Algorithmus II
for i = 0 ... spielerAnzahl-1
bester = i
for j = i+1 ... spielerAnzahl-1
if (spielerListe[bester].getPunkte() < spielerListe[j].getPunkte()) then
bester = j
endif
endfor
tausche Spieler i mit Spieler bester in spielerListe
endfor
- Gib jeweils an, welches Sortierergebnis nach der Ausführung der Algorithmen I und II bei der Anwendung auf die Highscore-Liste "vorher" vorliegt.
- Analysiere die beiden Algorithmen, und entscheide ob diese stabil sind.