Die Darstellung von ganzen Zahlen
Ein Mikroprozessorsystem verarbeitet immer Bitmuster in Einheiten zu 8, 16, 32 oder mehr Bit. Erst durch die Art der Verarbeitung wird diesem Bitmuster eine bestimmte Bedeutung zugewiesen. Wende ich einen arithmetischen Maschinenbefehl auf ein Bitmuster an, so wird es als Zahl interpretiert, eine Ausgabe auf den Bildschirm interpretiert das gleiche Bitmuster dagegen als darstellbares Zeichen des aktuellen Zeichensatzes.
Beispiel: Ein Byte hat den Inhalt 01000011b = 43h = 67d
Das kann unterschiedlich interpretiert werden.
- ASCII-Zeichen 'C'
- Vorzeichenlose oder vorzeichenbehaftete 8-Bit-Zahl: 67d = 43h
- als Maschinenbefehl
- Bitmuster um die Interrupts 0,1 und 6 freizugeben
Hier geht es um die Interpretation von Bitmustern ganze Zahlen betrachten.
Ein Mikroprozessor kann ein Bitmuster als Zahl interpretieren, dabei wird nach ganzen Zahlen mit und ohne Vorzeichen sowie Fließkommazahlen unterschieden.
Um die Darstellung der ganzen Zahlen zu verstehen, betrachten wir zunächst das uns geläufige Dezimalsystem , in dem zehn verschiedene Ziffern mit Potenzen der Zahl 10 gewichtet werden:
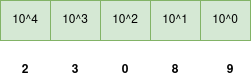
Ausgeschrieben bedeutet die Zahl: 2 * 10^4 + 3 * 10^3 + 0 * 10^2 + 8 * 10^1 + 9 * 10^0 = 2 * 10 000 + 3 * 1000 + 0 * 100 * 8 * 10 + 0 * 1. Jede Stelle hat also einen bestimmten Wert: Die ganz rechts hat den Wert 1, dann kommt der Wert 10, 100 u.s.w. Man spricht von einem Stellenwertsystem.
Da ein Mikroprozessorsystem nur 2 Zustände kennt, 0 und 1, verwendet man hier als Basis die Zahl 2 anstatt der gewohnten 10:

Ausgeschrieben bedeutet diese Zahl: 1 * 2^4 + 1 * 2^3 + 1 * 2^2 + 0 * 10^1 + 1 *2^0 = 16 + 8 + 4 + 0 + 1 = 29d
Übertrag
Mit n Bit kann man also die (vorzeichenlosen) Zahlen von 0-2^n-1 darstellen. Überschreitet man diesen Bereich, findet ein Übertrag statt - der Przessor setzt das Carry-Flag:
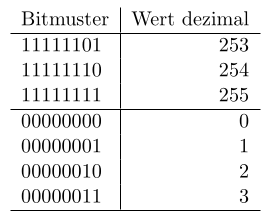
Addiert man zum Bitmuster von 255 '1', findet ein Übertrag von der Einer auf die Zweierstelle statt, von der Zweier- auf die Vierer u.s.w. da nur 8 Bit zur Verfügung stehen, ist das Ergebnis in 8 Bit nicht '1 0000 0000' (9 Bit) sondern '0000 0000'. Dieser Fehler wird im Carry-Flag festgehalten.
Negative Zahlen - Zweierkomplement
Negative Zahlen werden im Zweierkomplement notiert. Dabei hat das höchstwertige Bit ein negatives Vorzeichen:
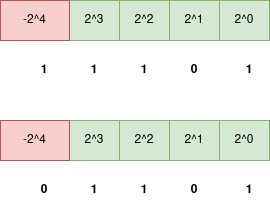
Die Zahl oben steht für - 1 * 2^4 + 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = -16 + 8 + 4 + 0 + 1 = -3d
Die Zahl unten steht für - 0 * 2^4 + 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = -0 + 8 + 4 + 0 + 1 = 13d
Eine negative Zahl hat also stets eine 1 an der höchstwertigen Stelle, denn die anderen Stellen können auf keinen Fall den neagtiven Wert ausgleichen: 1111 1111 = -1d
Zahlen mit der Länge 8 Bit im Zweierkomplement haben also einen Wertebereich von -128 … 127
Die Darstellung im Zweierkomplement führt zu "nahtloser" Addition negativer Zahlen:
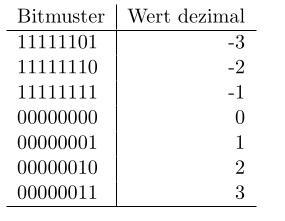
Addiert man zu -1 die Zahl 1 ergibt sich korrekterweise 0 - man muss lediglich das Carry-Flag ignorieren. Genau so rechnet ein Mikroprozessor.
Überlauf
Beim Rechnen mit Zahlen in Zweierkomplementdarstellung lauert eine andere Gefahr: Ein Übertrag auf das Vorzeichenbit, der sog. Überlauf ändert nämlich das Vorzeichen der Zahl! Dies passiert allerdings nur, wenn nicht gleichzeitig auch ein Übertrag entsteht und Mikroprozessoren setzen auch nur dann das Überlaufflag.
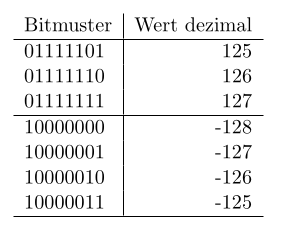
Bei der Addition von 1 zu 127 findet ein Überlauf auf das Vorzeichenbit statt, man erhält plötzlich -128 als Ergebnis.
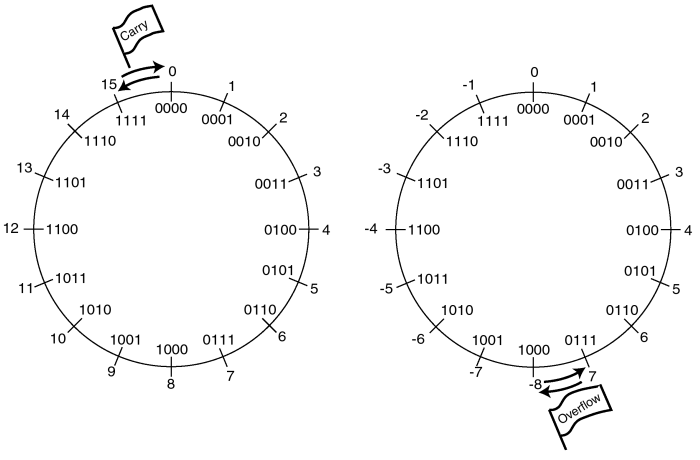
Zahlenringe für 4Bit-Zahlen
Unten sieht man eine recht intuitive Darstellung der Situation als "Zahlenring" für 4 Bit lange Binärzahlen. Links vorzeichenlose Zahlen mit dem Übertrag, rechts Zahlen in Zweierkomplementdarstellung mit Überlauf.
Zahl und Gegenzahl im Zweierkomplement
Wenn man zu einer gegebenen Zahl im Zweierkomplement die Gegenzahl bestimmen möchte, kann man wie folgt vorgehen:
1011ist-8 + 3 = -5d. Gesucht ist also die Binärdarstellung von+5d- Die invertierte Zahl ist
0100(4d) - Die Gegenzahl ist
0101(5d)
Das klappt immer!
$$-Z = \overline{Z} +1 $$