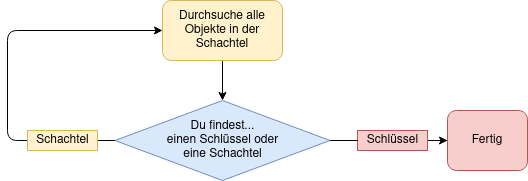
Rekursive Schachtelsuche
Die rekursive Denkweise macht sich zunutze, dass wir für jede Schachtel, wie wir finden, dasselbe tun müssen:
- Aufmachen.
- Wenn ein Schlüssel drin ist: Freuen!
- Wenn eine Schachtel drin ist: Das was wir mit jeder Schachtel machen…
funktion suche_schluessel(schachtel):
für jeden gegenstand in schachtel:
wenn gegenstand.istSchachtel():
suche_schluessel(gegenstand)
sonst wenn gegenstand.istSchlüssel:
ausgeben "Schlüssel gefunden!"
Bei der Betrachtung des Pseudocodes fällt auf, dass sich die Funktion suche_schlüssel selbst aufruft – das ist der Ausdruck im Code des Denkprinzips "das was wir mit jeder Schachtel machen" von oben.
Wenn eine Funktion sich selbst aufruft spricht man von Rekursion.
Ein Wort zu Eleganz und Performanz: Die rekursive Formulierung eines Algorithmus ist oft klarer als die iterative - sie bietet aber keine Performancevorteile – oft sind iterative Formulierungen sogar schneller.
Loops may achieve a performance gain for your program. Recursion may achieve a performance gain for your programmer. Choose which is more important in your situation!
(Leigh Caldwell, http://stackoverflow.com/a/72694/139117)
Fallunterscheidung ist unbedingt notwendig
Die Funktion ruft sich aber nicht bedingungslos selbst auf, sondern nur dann, wenn eine Schachtel (und kein Schlüssel) gefunden wird. Wenn man diese Fallunterscheidung weglässt, erzeugt man eine "rekursive Endlosschleife": Die Funktion ruft sich bedingungslos immer wieder selbst auf, das Programm kommt zu keinem Ende.

(A1) Experiment: Countdown
Implementiere eine Methode, die einen Countdown ausgibt:
4 ..... 3 ..... 2 ..... 1 ..... 0
(A) Zunächst iterativ, z.B. mit einer for-Schleife, in Java: public void countdown_iterativ (int start). Teste den Code - funktioniert dein Countdown?
(B) Dann rekursiv anhand des folgenden Pseudocodes:
countdown_rekursiv(int i): print(i + " .... ") countdown_rekursiv(i-1)
- Teste den Code. Was beobachtest du?
- Skizziere eine Programmablaufdiagramm für die rekursive Methode.
- Erläutere, was das Problem ist.
Jede rekursive Funktion benötigt eine Fallunterscheidung in zwei Fälle:
- Rekursionsfall: Im Rekursionsfall ruft sich die Funktion selbst auf
- Basisfall: Im Basisfall ruft sich die Funktion nicht selbst auf, die Rekursion wird mit einem
return-Statement beendet.
(C) Passe deine rekursive Methode anhand des folgenden Pseudocodes mit einer Fallunterscheidung an:
countdown_rekursiv(int i):
wenn i<0:
return
sonst:
print(i + " .... ")
countdown_rekursiv(i-1)
- Teste deinen Code
- Skizziere ein Programmablaufdiagramm für die rekursive Variante mit Fallunterscheidung.