Deterministische endliche Automaten
DEA ist die deutsche Abkürzung für Deterministischer Endlicher Automat. Im Englische lautet die Abkürzung DFA für Deterministic Final Automaton. Auch in deutschsprachiger Fachliteratur wird oft das Akronym DFA genutzt.
Definition
Ein DEA ist ein 5-Tupel DEA = { Q, Σ, δ, E, s} er besteht also aus den folgenden 5 Teilen:
QMenge aller Zustände (oft auch Z oder S (engl. state))ΣAlphabet / Menge der Alphabetzeichen (Sigma)δÜbergangsfunktion (Delta)EMenge der akzeptierenden Endzustände,sStartzustand.
Den Übergang von einem Zustand zum nächsten bezeichnet man auch als Transition oder Zustandsübergang.
Ein deterministischer endlicher Automat (deterministisch = klar definierte Zustände & Übergänge, daher reproduzierbare Verarbeitung) hat bestimmte Eigenschaften:
- Von einem Zustand q1 kann es keine 2 möglichen Übergänge geben, die beide dasselbe Alphabetzeichen verarbeiten. → Pro Alphabetzeichen gibt es nur einen möglichen Weg!
- Ebenso darf es nur einen einzigen Startzustand geben.
Das Wort endlich bezieht sich darauf, dass es eine endliche Menge von Zuständen gibt (also nicht unendlich viele).
Darstellung
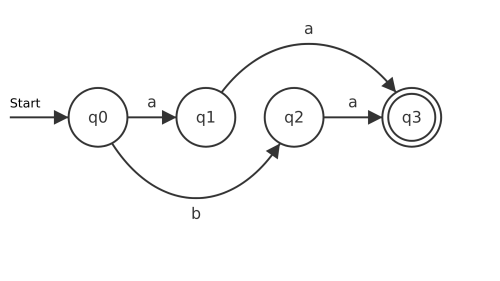
Ein DEA wird häufig durch seinen Übergangsgraphen dargestellt. Gelegentlich wird auch der Begriff Zustandsübergangsdiagramm verwendet.
Im Übergangsgraphen sind viele Informationen enthalten:
- Q={q0,q1,q2,q3}
- Σ={a,b}
- δ wird dargestellt durch die Pfeile, die von einem Zustand zum nächsten führen.
- E={q3}
- s=q0
Die Übergangsmatrix
Die Übergangsfunktion δ kann auch als Übergangsmatrix oder Übergangstabelle dargestellt werden. Dabei werden in der ersten Spalte alle Zustände eingetragen und in der ersten Zeile alle Zeichen des Eingabealphabets Σ eingetragen.
In den Tabellenzellen wird vermerkt, zu welchem Zustand der Automat wechselt, wenn er zuvor im Zustand der ersten Spalte war und dann die Eingabe der ersten Zeile erfolgt. Die Übergangstabelle für das obige Beispiel sieht also so aus:
| δ | a | b |
|---|---|---|
| q0 | q1 | q2 |
| q1 | q3 | |
| q2 | q3 | |
| q3 |
Das bedeutet im Beispiel: Wenn der Automat sich im Zustand q1 befindet, und es erfolgt die Eingabe a, wechselt er zum Zustand q3.
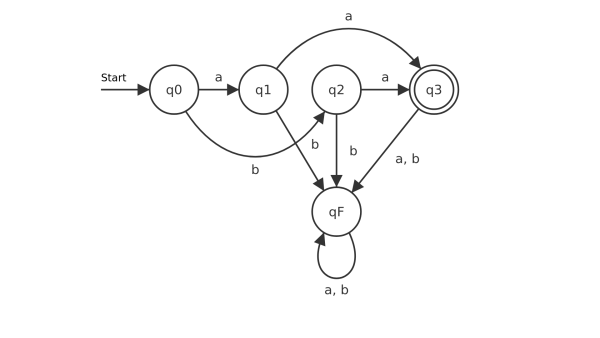
Nun fällt auf, dass die Tabelle unvollständig ist: Wenn der Automat sich im Zustand q1 befindet, und die Eingabe b erfolgt, ist kein Ziel angegeben, denn der Automat akzeptiert an dieser Stelle die Eingabe b überhaupt nicht. Das liegt daran, dass im Übergangsdiagramm der Fehlerzustand der Übersichtlichkeit halber weggelassen wurde. Das vollständige Diagramm sieht so aus:
Die vollständige Übergangsmatrix sieht also so aus:
| δ | a | b |
|---|---|---|
| q0 | q1 | q2 |
| q1 | q3 | qF |
| q2 | q3 | qF |
| q3 | qF | qF |
| qF | qF | qF |
Während man in Zustandsübergangsdiagrammen den Fehlerzustand meist weglässt, um die Übersichtlichkeit zu verbessern, wird der Fehlerzustand bei der Darstellung von δ als Übergangsmatrix für gewöhnlich angegeben.

(A1)
Gegeben ist der folgende DEA: M = ({z0,z1,z2,z3}, {apfel,birne}, δ, {z0}, z3). δ ist in Form einer Übergangstabelle gegeben:
| δ | apfel | birne |
|---|---|---|
| z0 | z1 | z3 |
| z1 | z2 | z0 |
| z2 | z3 | z1 |
| z3 | z0 | z2 |
- Welches sind die Zustände des DEA, was der Start, was gültige Endzustände?
- Erstelle ein Zustandsübergangsdiagramm für den DEA

(A2)
Entwickle einen DEA, der als Eingabemenge Σ={0,1} hat, und alle Eingaben akzeptiert, die auf 10 enden.
- Gib einen Übergangsgraphen an
- Gib eine Darstellung als Übergangsmatrix an
Beispieleingaben:
(A3)
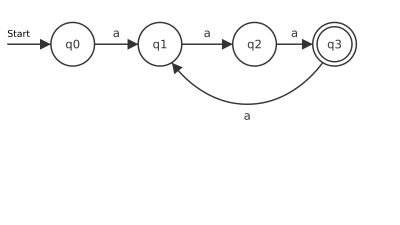
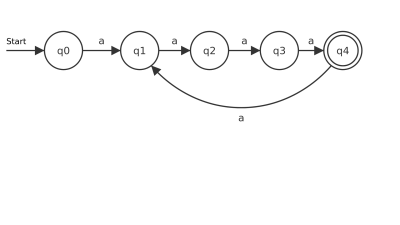
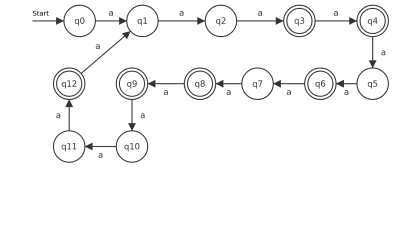
Es soll ein DEA entworfen werden, der alle Worte der Form an (also a, aa, aaa, aaaa, u.s.w.) versteht, wobei n durch 3 oder durch 4 (oder durch beide) teilbar ist.
- Gib einen Übergangsgraphen an
- Gib eine Darstellung als Übergangsmatrix an
Beispieleingaben:
aaa wird akzeptiert aaaa wird akzeptiert aaaaa wird nicht akzeptiert aaaaaa wird akzeptiert
Material
| Filename | Filesize | Last modified |
|---|---|---|
| as0.png | 100.2 KiB | 24.05.2022 13:21 |
| as01.png | 104.2 KiB | 24.05.2022 13:22 |
| as2.png | 180.1 KiB | 24.05.2022 13:25 |
| beispiel.png | 122.8 KiB | 20.05.2022 13:49 |
| beispiel1.png | 127.7 KiB | 20.05.2022 14:11 |
| folien_fs_dea.odp | 177.0 KiB | 23.05.2022 17:01 |
| folien_fs_dea.pdf | 250.8 KiB | 23.05.2022 17:01 |