Kellerautomaten und Klammersprachen
(A1) Vorüberlegungen
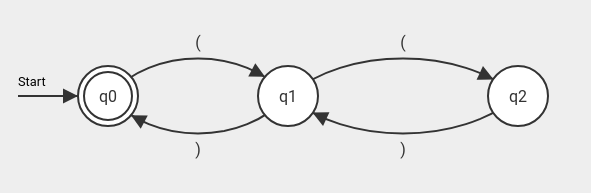
(A) Konstruiere einen endlichen Automaten, der die Sprache LKlammer2 aller Klammerausdrücke der Tiefe 2 erkennt. Zur Sprache gehören z.B.
(()), ()(), (), (()())
Nicht zur Sprache gehören z.B.
((()), ((())), ()), )(, )()(
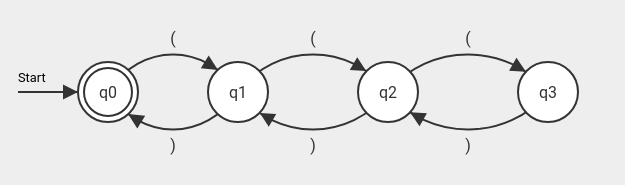
(B) Gibt es einen endlichen Automaten A, der die Sprache L() = {(n)n | n = 1, 2, 3, …} erkennt? Wie sehen diese aus und worin unterscheiden sich die Automaten, die unterschiedliche Klammerungstiefen erkennen?
(C) Gib einen endlichen Automaten A an, der die allgemeine Klammersprache, also Klammerungen beliebiger Tiefe erkennt - siehst du ein Problem?
Der Kellerautomat am Beispiel
Wir erweitern den endlichen Automaten um einen Speicher, der (potentiell) unbegrenzt viele Daten aufnehmen kann. Für kontextfreie Sprachen reicht als Speicher ein Stack – dieser wird auch als "Keller" bezeichnet, aus diesem Grund nennt man solche um einen Stack erweiterten DEAs "Kellerautomat".
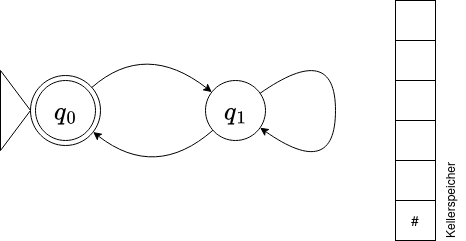
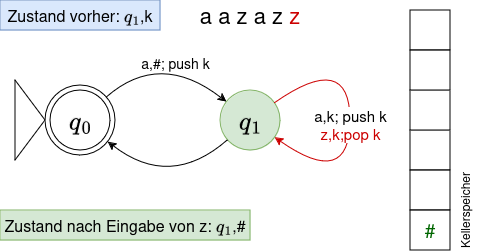
Für unsere Klammersprache könnte ein erster Entwurf eines Kellerautomaten so aussehen - der Kellerspeicher ist hier mit 6 "Speicherplätzen" gezeichnet, kann aber durch weiteres "auf den Stack legen" beliebig erweitert werden:
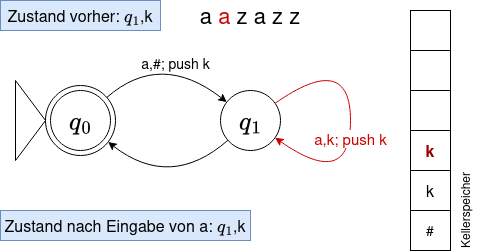
Zu Beginn ist der Kellerspeicher leer - das wird durch das Symbol # gekennzeichnet - der Ablauf beginn beim markierten Startknoten. Der Automat befindet sich also zu Beginn im Zustand q0,#
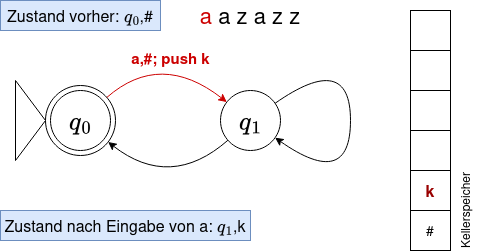
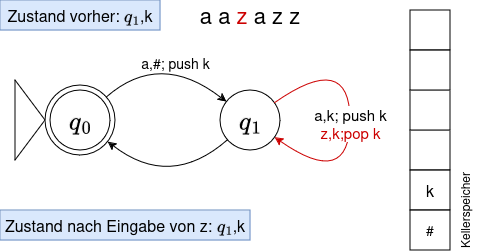
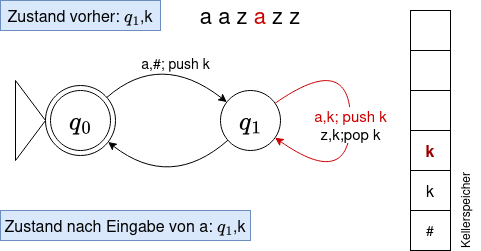
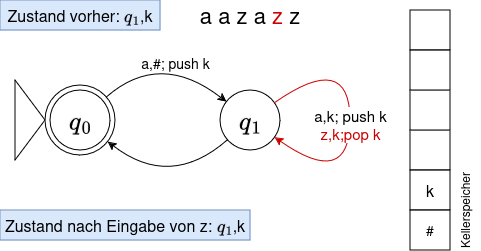
Um Komplikationen beim Aufschreiben der Klammern zu vermeiden, verwenden wir von nun an für eine öffnende Klammer das Symbol a, für eine schließende Klammer ein z. Wir wollen nun nachvollziehen, ob das Wort aazazz vom Automaten akzeptiert wird - und vor allem, was der Automat dabei alles "tun" muss.
- Wir müssen bei jedem Übergang von einem Zustand in einen anderen nun auch noch unseren Speicher "bedienen". Der Speicher kennt 3 Operationen:
- Etwas auf den Stack legen push
- Das oberste Element vom Stack herunter nehmen pop
- Den Stack unverändert belassen noop
- Welche Speicheroperation wir bei einem Zustandsübergang ausführen hängt nicht nur von der Eingabe ab, sondern kann außerdem vom Zustand des Stacks abhängen. Ist der Stack leer, welches Element liegt oben?
Schritt für Schritt - wir bauen einen Kellerautomaten
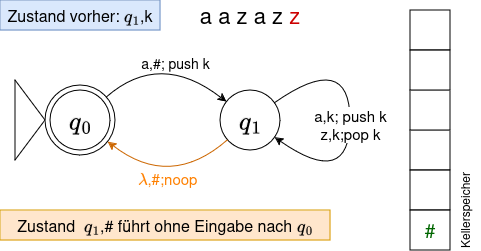
Das stellt ein kleines Problem dar: Dieser Zustand signalisiert, dass das Eingabewort vom Automaten akzeptiert wird, denn hier kommen wir nur dann an, wenn wir gleich viele Klammern geöffnet haben wie wir geschlossen haben - q1,# ist gewissermaßen ein akzeptierender Endzustand, q1 alleine kann aber keiner sein.
Formale Darstellung eines Kellerautomaten
Ein Kellerautomat ist ein 6 Tupel, besteht also aus 6 Bestandteilen A={∑,Q,s,E,δ,Γ}3)
| Allgemein | Am Beispiel |
|---|---|
| Eingabealphabet ∑ | ∑ = {a, z} |
| Menge Q von Zuständen | Q = {q0,q1,qF} (incl. Fehlerzustand!) |
| Startzustand s ∈ Q | s = q0 |
| E ⊆ Z von Endzuständen | E = {q0} |
| Übergangsfunktion δ hängt meist von mehreren Krtiterien ab | Hängt von drei Kriterien ab, muss deswegen zeilenweise angegeben werden (s.u.) |
| Stackalphabet Γ (Gamma) | Γ ={#, k}; das # steht für einen leeren Stack |
Die Übergangsfunktion δ für unser Beispiel kann zeilenweise wie folgt angegeben werden:
| Kriterien | Auswirkung | ||||
|---|---|---|---|---|---|
| alter Zustand? | Eingabe? | auf Stack? | → | neuer Zustand | Operation |
| q0 | a | # | → | q 1 | push k |
| q1 | a | k | → | q 1 | push k |
| q1 | z | k | → | q 1 | pop k |
| q1 | λ | # | → | q 0 | nop |
Ablaufprotokoll eines Kellerautomaten
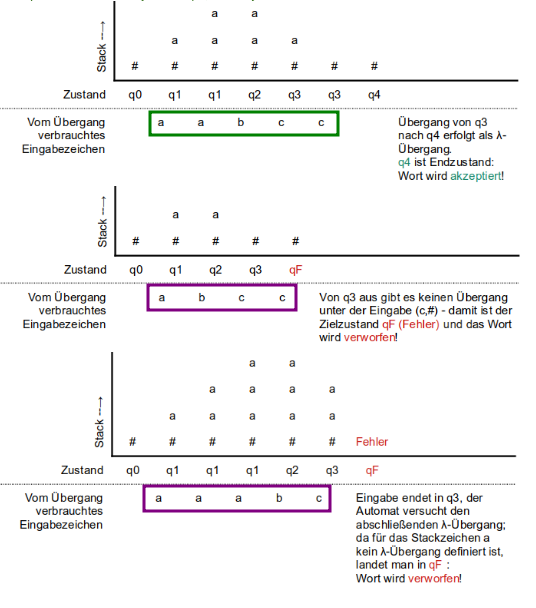
Der "Lauf" eines Kellerautomaten bei der Verarbeitung einer Eingabe kann in einem Ablaufprotokoll dokumentiert werden, wobei die durchlaufenen Zustände, die Entwicklung des Stack und das Verbrauchen der Eingabe sichtbar werden sollten. Dazu eignet sich beispielsweise die Darstellung als Tabelle - hier für unsere Beispieleingabe aazazz:
| Stack | ||||||||
| k | k | |||||||
| k | k | k | k | k | ||||
| # | # | # | # | # | # | # | # | |
| Zustand | q0 | q1 | q1 | q1 | q1 | q1 | q1 | q0 |
| Vom Übergang verbrauchtes Eingabezeichen | a | a | z | a | z | z |
Eingabe endet, q0 ist Endzustand: Wort wird akzeptiert!
Aufgaben
(A2)
- Simuliere den Klammerautomaten in FLACI.
- Teste den Automaten mit verschiedenen Eingaben und vollziehe seine Funktionsweise nach.
Hinweise
Flaci verwendet eine geringfügig andere Darstellung als unser Beispiel, außerdem stellt es die Stack Operationen nicht direkt zur Verfügung.
- Du musst einen DPA oder einen DKA erzeugen, je nach Spracheinstellung deines Browsers.
- Bei der Darstellung des Übergangs verwendet Flaci folgende Konvention:
(Stacksymbol, Eingabezeichen):Erstetzung für das Stacksymbol(X,g):XX: push X. Wenn das oberste Element des Stacks ein X ist und ein g eingegeben wird, wird X durch XX ersetzt, es wird also ein X auf den Stack gelegt.(X,b):ε: pop. Wenn das oberste Element des Stacks ein X ist und ein b eingegeben wird, wird X durch "nichts" (ε) ersetzt.(X,p):X: noop. Wenn das oberste Element des Stacks ein X ist und ein p eingegeben wird, wird X durch X ersetzt, es passiert also nichts.
(A3)
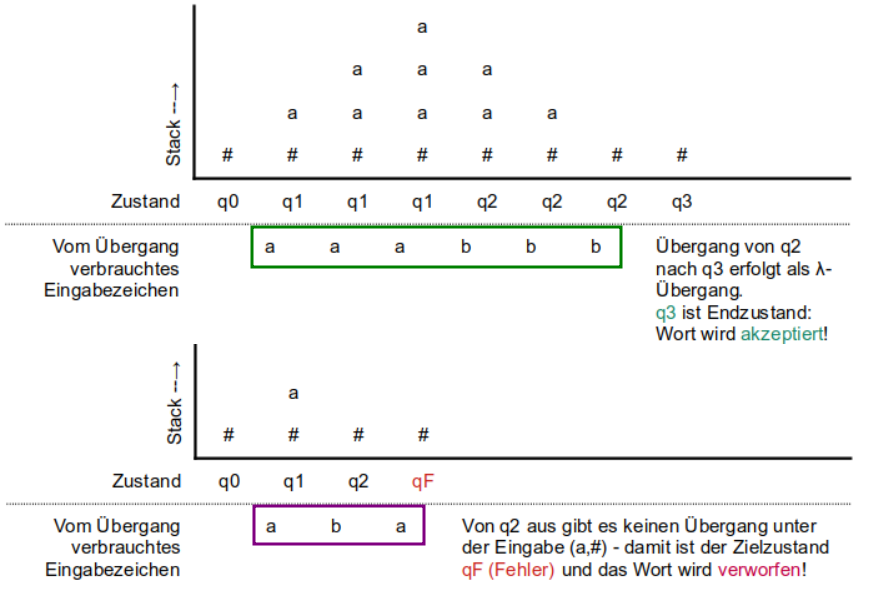
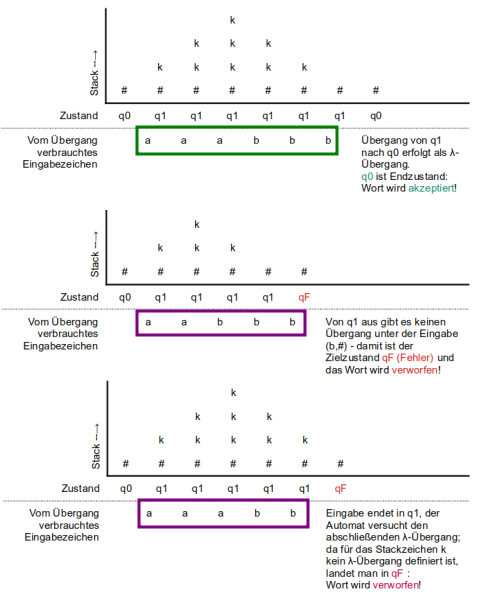
Gegeben sind folgende Kellerautomaten. Beschreibe für jeden der Automaten die Wörter, die dieser erkennt und erstelle jeweils Ablaufprotokolle für zwei aussagekräftige Beispieleingaben – ein Wort, das akzeptiert wird und eines, das verworfen wird.
(A)
(B)
(C)
(A4)
Entscheide mit Hilfe eines Kellerautomaten, ob die folgenden Sprachen kontextfrei sind. Sprachen sind kontextfrei, wenn sie von einem Kellerautomaten erkannt werden können. Wenn die Sprache kontextfrei ist, dann erläutere, wie der Kellerautomat arbeiten würde. Falls nicht, dann begründe, warum sie nicht mit einem Kellerautomaten erkannt werden kann.
- (A) L = { anbn | n ≥ 0 }
- (B) L = { anbncn | n ≥ 0 }
- (C) L = { w ∈ {a, b}* | #a = #b } die alle Wörter enthält, die aus gleich vielen a und b bestehen, die – im Gegensatz zur Sprache aus Aufgabenteil a) - in beliebiger Reihenfolge auftreten dürfen. (Hinweis: #a bezeichnet die Anzahl der a´s in dem betreffenden Wort.)
- (D) L = { anbmcn | n, m ≥ 0 }
(A5) Zusatzaufgabe
Implementiere zunächst einen endlichen Automaten der die Klammersprache L2 aus dem Eingangsbeispiel erkennt, Arbeite mit a und z für Klammer auf und Klammer zu.
- Die Eingabe soll als Parameter beim Erstellen des Automaten erfragt werden.
- Modelliere die Zustände des Automaten und gib bei der Bearbeitung der Eingabe die Zustandswechsel auf den Konsole aus, so dass der Ablauf bei der Verarbeitung der Eingabe erkennbar ist.
- Erweitere den Automaten um einen Stack, um unendlichen Klammertiefen zu erkennen. erstelle bei der Verarbeitung der Eingabe ein Ablaufdiagramm wie oben, das du auf der Konsole ausgibst.