Mealy-Automaten

Buch erstellen
Diese Seite zum Buch hinzufügen

Buch erstellen
Diese Seite aus Buch entfernen

¹⁾

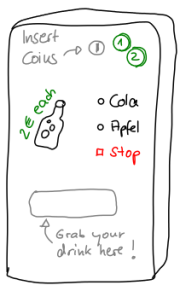
Die sogenannten Mealy-Automaten können in jedem Schritt außer der Änderung des internen Zustands auch eine Ausgabe erzeugen und erlauben damit die Modellierung z.B. von Getränke-, Fahrkarten- oder ähnlichen Automaten, die wir aus unserer Umwelt kennen.

Als Beispiel soll ein Getränkeautomat dienen, der…

… die Tasten A, C und S hat (für Apfelsaft, Cola und Stop)
… 1EUR- und 2EUR-Münzen annimmt.

Damit ist sein Eingabealphabet Σ = {c, a, s, 1, 2}. Anders als ein DEA bewirkt bei einem Mealy-Automaten jede Eingabe eine Ausgabe, das Ausgabealphabet Δ = {"Guthaben 1€", "Guthaben 2€", "1€" , "2€", "Apfelsaftflasche", "Colaflasche"}

Eine Mealy-Maschine oder ein Mealy-Automat ist durch ein 6-Tupel M = (Q,Σ,∆,δ,λ,q₀) definiert.

Die verwendeten Symbole haben folgende Bedeutungen:

Q: endliche Menge der Zustände
Σ: Eingabealphabet
∆: Ausgabealphabet
δ: totale Überführungsfunktion Q x Σ → Q
λ: totale Ausgabefunktion Q x Σ → ∆
q0: Anfangszustand, q0 ∈ Q

Die Maschine erzeugt in jedem Übergang eine Ausgabe.

Die Überführungsfunktion δ und die Ausgabefunktion λ können wie beim DEA auch, in einem Übergangsgraphen dargestellt werden. Ein passender Übergangs- oder Transitionsgraph sieht folgendermaßen aus:

Anders als beim DEA muss zu jedem Übergang außer der Eingabe auch die Ausgabe notiert werden, dies geschieht für gewöhnlich durch ein Trennzeichen wie ; oder /.

Der Automat befindet sich immer in genau einem der Zustände und beginnt dabei immer im so genannten Startzustand, der mit einem zusätzlichen Pfeil gekennzeichnet wird (hier q0).

Jede Eingabe bewirkt einen Übergang (auch Transition genannt) zu einem anderen Zustand, dargestellt durch einen Pfeil.

Bei Mealy-Automaten gehört zu einem Übergang auch eine Ausgabe.

Vom Startzustand q0 aus wird durch Einwurf von 1€ der Zustand q2 erreicht und die Ausgabe Guthaben: 1,00 erzeugt.

Nachfolgende Aufgaben können teilweise sowohl mit der Webseite FLACI, also auch mit dem Java-Tool JFLAP bearbeitet werden!

(A1)

Bearbeitung mit FLACI

Bearbeitung mit JFLAP

Und wie bei DEAs kann man die Übergangsfunktion δ und die Ausgabefunktion λ auch hier als Übergangsmatrix/Übergangstabelle darstellen, anstelle des Übergangsgraphen. Wie bei den DEAs gilt: Im Graph kann man den Fehlerzustand der Übersichtlichkeit wegen weglassen, in der Übergangsmatrix wird dieser stets angegeben.

Ausgangszustand	1€	c
	Eingaben → (Folgezustand / Ausgabe)
q0	q2/"Guthaben 1€"
q1
q2
qF		qF

(A2)

Vervollständige anhand des Übergangsgraphen die Übergangsmatrix

(A3)

Falls du mit FLACI arbeitest:
Schalte die Option δ und λ als partielle Funktionen in FLACI aus und ergänze den Automaten in FLACI um den Fehlerzustand. Überprüfe so deine Tabelle aus der vorigen Aufgabe.

(A4)

Gib eine Eingabe an, die zur Ausgabe Apfelsaftflasche führt.

(A5)

Gib die Ausgabe an, die zur Eingabe 1€,s gehört. In welchem Zustand befindet sich der Automat anschließend?

(A6)

Modelliere einen Mealy-Automaten für einen Automaten aus der Schule. Gib die folgenden Informationen an:

Eingabealphabet, Zustandsmenge, Startzustände und Ausgabealphabet
Zustandsübergangs- und Ausgabefunktionen als Tabelle
Zustandsübergangsgraph

(A7)

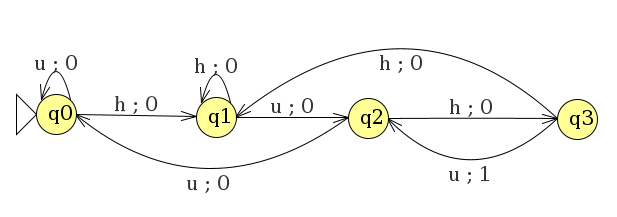
Ein Mealy-Automat A ist durch den folgenden Übergangsgraphen gegeben:

Gib die Ausgabe zur Eingabe uhuhuhuuhhuhu an
Beschreibe A als 6-Tupel. Lege die Übergangsfunktion δ sowie die Ausgabefunktion λ durch eine Tabelle fest.
Beschreibe die "Übersetzungsfunktion" - wann gibt der Automat eine 1 aus?

¹⁾

Diese Wiki-Seite basiert auf Material der ZPG INformatik/BW und steht unter einer CC-BY-NC-SA Lizenz. Als Autoren sind angegeben "Dietrich, Lautebach (2020)".