Festkommazahlen
Wir haben nun eine Darstellung für natürliche und – mit dem Zweierkomplement – eine für ganze Zahlen im Binärsystem gefunden. Offen ist die Frage wie man Brüche/Kommazahlen im Binärsystem darstellen kann?
Eine erste Möglichkeit, bei der alle bisherigen Rechenregeln erhalten bleiben, stellt die Darstellung als Festkommazahl dar. Der größte Vorteil bei dieser Darstellung ist, dass dieselbe ALU1) des Rechners, die die ganzzahligen Berechnungen durchführt auch mit dieser Darstellung umgehen kann, man benötigt im Prozessor also kein neues Rechenwerk für diese Art der Kommazahlen.
Wie funktionierts?
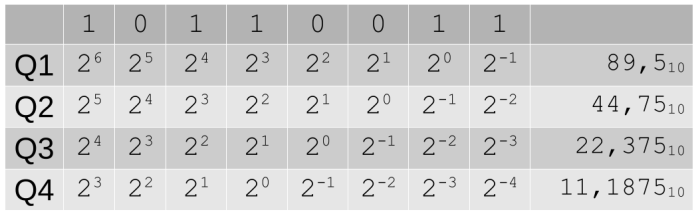
Bei der Festkommadarstellung wird im Vorfeld definiert, an welcher Stelle sich das Komma befindet, bzw. wie viele Vorkomma- und wie viele Nachkommastellen die Zahl beinhaltet. Das wird mit der Bezeichnung Q<n> angegeben:
- Q1: Eine Nachkommastelle
- Q2: zwei Nachkommstellen
- Q3: drei Nachkommastellen
- Q4: Vier Nachkommastellen
- Q5: …
Die Wertigkeit hinter der Kommastelle wird entsprechend der 2er-Potenzen fortgeführt.
Bei fester Bitlänge der gesamten Zahl wird also mit wachsender Anzahl der Nachkommastellen der Wertebereich vor dem Komma kleiner.
(A1)
- Bestimme die dezimalen Werte aller Nachkommastellen bei Q4.
- Welche Einschränkung ergibt sich daraus für Zahlen, die in Q2 dargestellt werden können?
- Kann man die Zahl 8,3 in Q3 darstellen?
- Kannst du eine Regel formulieren, welche Zahlen man in der Festkommadarstellung darstellen kann? Denke daran, dass alle endlichen Dezimalzahlen als Bruch geschrieben werden können.
(A2)
Rechne die Zahlen im Binärsystem Q4 angegebenen Zahlen ins Dezimalsystem um - oder andersrum:
- 10101100b = ?? d
- 00010001b = ?? d
- 6,375d = ?? b
- 9,9375d = ?? b
(A3)
- Bestimme den Zahlbereich, der sich mit 8 Bit in Q4 darstellen lässt.
- Welche Differenz haben in dieser Darstellung zwei nebeneinander liegende Zahlen? Wie kann man diese "Genauigkeit" allgemein berechnen?
- Erläutere, warum man 0,1d nur näherungsweise als Festkommazahl darstellen kann.
(A4)
Berechne die Summe (binär) zweier Q4-Zahlen und kontrolliere das Ergebnis, indem du alle Werte ins Dezimalsystem umrechnest.
(i)
00111100b 01000101b
(ii)
00011000b 00001000b
(A5)
- Berechne mit schriftlicher Multiplikation das Produkt der beiden Q4-Zahlen. Vergleiche dein Ergebnis mit den Dezimalzahlen:
00001000b∙00010000b = - Warum liefert die schriftliche Multiplikation ein falsches Ergebnis? Wie muss man dieses korrigieren?
Material
| Filename | Filesize | Last modified |
|---|---|---|
| auswahl_272.png | 39.1 KiB | 14.09.2022 14:27 |
| festkomma.odp | 56.0 KiB | 14.09.2022 16:07 |
| festkomma.pdf | 65.7 KiB | 14.09.2022 16:07 |