(A1)
Untersuche im Graphentester den Algorithmus "MST (Kruskal)" zur Bestimmung des minimalen Spannbaums auf der Karte der größten Städte in Deutschland (02_deutschlandkarte.csv im Ordner 08_minimalspanningtree).
Beschreibung des Algorithmus von Kruskal
Der Algorithmus verfolgt die Idee, immer die kürzeste Kante des Graphen dem Baum hinzuzufügen, wenn dadurch nicht ein Zyklus entsteht und die Kante damit überflüssig ist. Es entstehen dabei zunächst viele einzelne Bäume (ein Wald), die sukzessive zu einem einzigen Baum zusammengeführt werden. Um die Zyklen leicht erkennen zu können, werden die Knoten jedes einzelnen Baums in einer eigenen Farbe eingefärbt.
Zunächst werden die Kanten also nach ihrem Gewicht sortiert und dann für jede Kante folgende Regeln beachtet:
Außer in Fall 4 wird außerdem die Kante markiert, da sie zum minimalen Spannbaum gehört.
1)
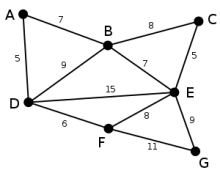
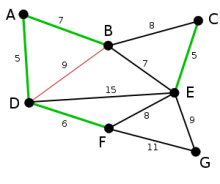
Dies ist der Graph, zu dem der Algorithmus von Kruskal einen minimalen Spannbaum berechnen wird. Die Zahlen bei den einzelnen Kanten geben das jeweilige Kantengewicht an. Zu Beginn ist noch keine Kante ausgewählt.
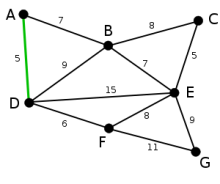
Die Kanten AD und CE sind die kürzesten (noch nicht ausgewählten) Kanten des Graphen. Beide können ausgewählt werden. Hier wird zufällig AD ausgewählt. (Dass diese keinen Kreis bildet, ist im ersten Schritt selbstverständlich.)
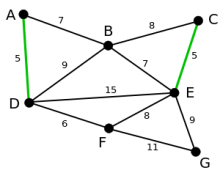
Nun ist CE die kürzeste, noch nicht ausgewählte Kante. Da sie mit AD keinen Kreis bildet, wird sie nun ausgewählt.
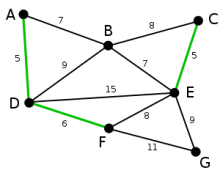
Die nächste Kante ist DF mit Länge 6. Sie bildet mit den schon gewählten Kanten keinen Kreis und wird deshalb ausgewählt.
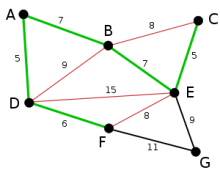
Jetzt könnten die Kanten AB und BE, jeweils mit Länge 7, ausgewählt werden. Es wird zufällig AB gewählt. Die Kante BD wird rot markiert, da sie mit den bis jetzt gewählten Kanten einen Kreis bilden würde und somit im weiteren Verlauf des Algorithmus nicht mehr berücksichtigt werden muss.
BE ist nun mit Länge 7 die kürzeste der noch nicht ausgewählten Kanten und da sie mit den bisher gewählten keinen Kreis bildet, wird sie ausgewählt. Analog zur Kante BD im letzten Schritt werden jetzt die Kanten BC, DE und FE rot markiert.
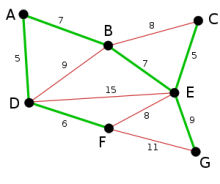
Als letzte wird die Kante EG mit Länge 9 ausgewählt, da alle kürzeren bzw. gleich langen Kanten entweder schon ausgewählt sind oder einen Kreis bilden würden. Die Kante FG wird rot markiert. Da nun alle nicht ausgewählten Kanten einen Kreis bilden würden (sie sind rot markiert) ist der Algorithmus am Ende angelangt und der grüne Graph ist ein minimaler Spannbaum des zugrundeliegenden Graphen.

(A2)
Übersetze die Beschreibung aus Aufgabe 1 in Pseudocode.
Pseudocode Kruskal
Minimal spanning tree:
Setze farbnummer auf 1
Hole eine Liste aller Kanten und sortiere sie aufsteigend
Wiederhole für jede Kante
k1 = Startknoten, k2 = Zielknoten der Kante
Falls Farbe von k1==0 und Farbe von k2==0
Setze Farbe beider Knoten auf farbnummer
Markiere die Kante
Erhöhe die Farbnummer um 1
Sonst
Falls Farbe eines Knotens==0
Setze Farbe dieses Knotens auf die des anderen
Markiere die Kante
Sonst
Falls beide Knoten unterschiedliche Farben haben
Wiederhole für jeden Knoten k im Graph
Falls Farbe von k die Farbe von k2 hat
Setze Farbe von k auf die Farbe von k1
Ende-Falls
Ende-Wiederhole
Markiere die Kante
Sonst
Lösche Kante
Ende-Falls
Ende-Falls

(A3)
Implementiere eine eigene Version des Kruskal-Algorithmus im Graphentester.
Lösungsvorschlag
int farbe = 1;
List<Kante> kanten = g.getAlleKanten();
List<Knoten> knoten = g.getAlleKnoten();
Collections.sort(kanten);
for (Kante k: kanten) {
int f1 = k.getStart().getFarbe();
int f2 = k.getZiel().getFarbe();
if(f1 == 0 && f2 == 0) {
k.getStart().setFarbe(farbe);
k.getZiel().setFarbe(farbe);
k.setMarkiert(true);
farbe++;
} else
if(f1 == 0) {
k.getStart().setFarbe(f2);
k.setMarkiert(true);
} else
if(f2 == 0) {
k.getZiel().setFarbe(f1);
k.setMarkiert(true);
} else
if(f1 == f2) {
k.setGeloescht(true);
} else
{
for(Knoten k1 : knoten) {
if(k1.getFarbe() == f2) k1.setFarbe(f1);
}
k.setMarkiert(true);
}
}