Minimalspannende Bäume
Muddy-City
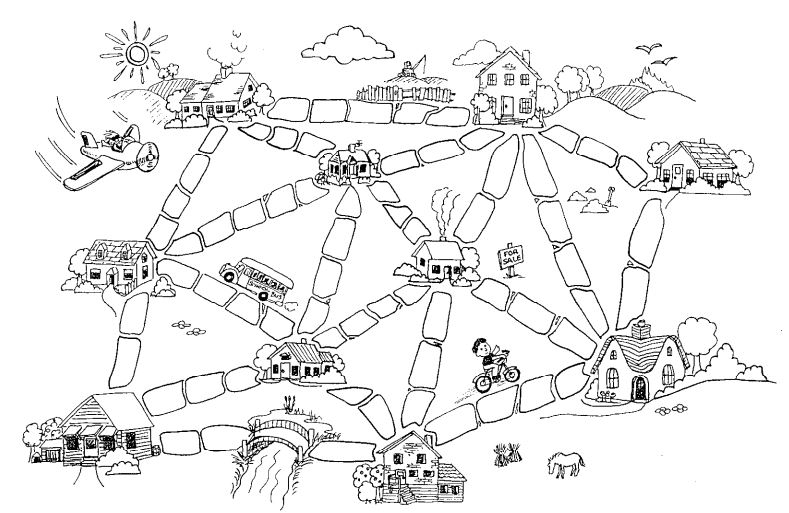
Vor langer Zeit gab es eine Stadt, die keine Straßen hatte. Sich in dieser Stadt zu bewegen war insbesondere dann schwierig, wenn der Regen nach starken Gewittern die Wege sehr matschig machte. Fahrzeuge blieben stecken und jeder hatte ziemlich dreckige Schuhe. Daher entschied der Bürgermeister, einige Straßen zu asphaltieren. Allerdings wollte er nicht mehr Geld ausgeben als unbedingt nötig, damit auch noch ein Schwimmbad gebaut werden konnte.
Also legte er zwei Bedingungen fest:
- Es müssen ausreichend Straßen asphaltiert werden, damit jeder von seinem Haus jedes andere Haus trockenen Fußes erreichen kann.
- Das Asphaltieren soll so wenig kosten wie möglich. Die Anzahl der Pflastersteine ist das Maß für die Kosten.
Aufgaben zum Muddy-City-Problem

(A1)
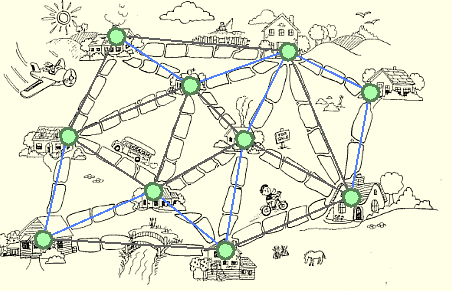
Finde die Wege, die alle Häuser miteinander verbinden und deren Asphaltierung am wenigsten kostet (=Pflastersteine beinhaltet).

(A2)
Welche Strategien hast du genutzt, um das Problem zu lösen?
Das Minimaler Spannbaum Problem (Minimal spanning tree)
Gegeben ist ein zusammenhängender, gewichteter, ungerichteter Graph.
Gesucht ist die Teilmenge der Kanten, so dass der Graph zusammenhängend bleibt und die Summe der Kantengewichte möglichst klein ist.
Vertiefung: Fragen & Aufgaben

(A3)
Wende den Algorithmus "MST (Prim)" zur Bestimmung des minimalen Spannbaums im Graphentester auf die Karte der größten Städte in Deutschland an (02_deutschlandkarte.csv im Ordner 08_minimalspanningtree). Beachte, dass nur markierte Kanten sichtbar sind, da es zu viele Kanten gibt, um sie alle übersichtlich darzustellen. Vergleiche mit dem Autobahnnetz in Deutschland. Nenne Ursachen für Unterschiede.

(A4)
Öffne den Stadtplan von Baden-Baden (03_badenbaden.csv) und die Karte mit den Fährstrecken (04_inseln.csv) jeweils im Graphentester. Lass dir auch hier mit dem Algorithmus MST (Prim) einen minimalen Spannbaum anzeigen (Achtung, die Kanten werden ungünstigerweise in blau gefärbt und sind kaum zu sehen). Gib je eine realitätsnahe Problemstellung für diese Graphen an, bei denen ein minimaler Spannbaum die beste Lösung ist.
Anders ausgedrückt: Für was bräuchte man in der Realität jeweils so einen minimalen Spannbaum? Für was für Probleme oder Anwendungen kann das relevant sein?
Zwei Algorithmen
Wir betrachten zwei Algorithmen zur Lösung des Problems des minimal spannenden Baums:
Weitere Fragen und Aufgaben

(A5)
Untersuche, ob die Algorithmen zur Bestimmung des minimalen Spannbaums auch mit negativen Kantengewichten zurechtkommen.

(A6)
Begründe, warum es sich bei den Algorithmen zur Bestimmung des minimalen Spannbaums um Greedy-Algorithmen handelt.
Näherungslösung für das TSP mit MST Algorithmen

(A7)
Beim Traveling Salesman Problem (TSP) sucht man nach der kürzesten Route durch eine gegebene Liste von Städten, die ein Handlungsreisender besuchen muss. Am Ende soll er wieder zu Hause ankommen.
Für dieses Problem kennt man keinen effizienten Algorithmus. Man kann aber die Algorithmen zur Bestimmung eines MST abändern, so dass sie eine Näherungslösung für das TSP darstellen.
Beschreibe die Veränderungen die am Algorithmus für den MST notwendig sind, um das TSP zu lösen. Du kannst dazu im Graphentester die Algorithmen TSP (Greedy: Knoten) und TSP (Greedy: kürzeste Kante) zu Hilfe nehmen.