(A1)
Untersuche im Graphentester den Algorithmus "MST (Prim)" zur Bestimmung des minimalen Spannbaums mit der Insel-Karte (04_inseln.csv im Ordner 08_minimalspanningtree).
Beschreibung des Algorithmus von Prim
Dieser Algorithmus startet mit einem beliebigen Knoten. Dieser wird markiert. Sukzessive werden an diesen Knoten weitere Knoten angebunden und so allmählich ein immer größerer Baum aufgebaut. Dabei wird derjenige Knoten dem Baum hinzugefügt, zu dem die kürzeste Kante vom bisherigen Baum führt. Diese Kante wird markiert.
Auch hier startet man damit, die Kanten nach ihrem Gewicht zu sortieren. Nun sucht man in dieser Liste nach einer Kante, bei der ein Knoten markiert ist und der andere nicht. Dabei kann man alle Kanten, bei denen beide Knoten markiert sind, streichen, da sie nie mehr gebraucht werden.
Hat man eine derartige Kante gefunden, wird sie markiert und aus der Liste entfernt. Der neu angebundene Knoten wird ebenfalls markiert. Diese Schritte wiederholt man, bis alle Knoten angebunden sind, also n-1 mal bei n Knoten.
1)
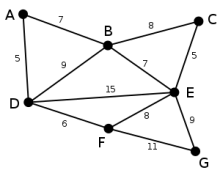
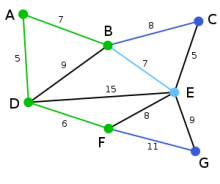
Dies ist der Graph, zu dem der Algorithmus von Prim einen minimalen Spannbaum berechnet. Die Zahlen bei den einzelnen Kanten geben das jeweilige Kantengewicht an.
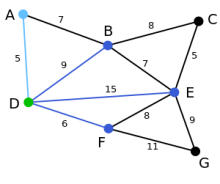
Als Startknoten für den Spannbaum T wird der Knoten D gewählt. (Es könnte auch jeder andere Knoten ausgewählt werden.)
Mit dem Startknoten können die Knoten A,B,E und F jeweils unmittelbar durch die Kanten DA, DB, DE und DF verbunden werden.
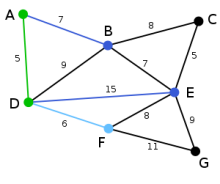
Unter diesen Kanten ist DA diejenige mit dem geringsten Gewicht und wird deshalb zusammen mit dem Knoten A zum Graphen T hinzugefügt.
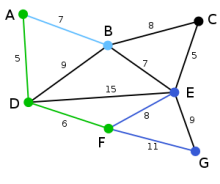
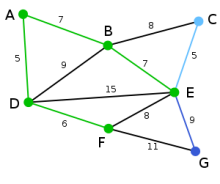
Mit dem bestehenden Graphen T kann der Knoten B durch die Kanten AB oder DB, der Knoten E durch die Kante DE und der Knoten F durch die Kante DF verbunden werden. Unter diesen vier Kanten ist DF diejenige mit dem geringsten Gewicht und wird deshalb zusammen mit dem Knoten F zum Graphen T hinzugefügt.
Mit dem bestehenden Graphen T kann der Knoten B durch die Kanten AB oder DB, der Knoten E durch die Kanten DE oder FE und der Knoten G durch die Kante FG verbunden werden. Unter diesen Kanten ist AB diejenige mit dem geringsten Gewicht und wird deshalb zusammen mit dem Knoten B zum Graphen T hinzugefügt.
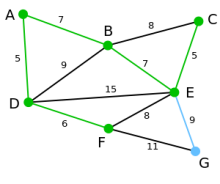
Mit dem bestehenden Graphen T kann der Knoten C durch die Kante BC, der Knoten E durch die Kanten BE, DE oder FE und der Knoten G durch die Kante FG verbunden werden. Unter diesen Kanten ist BE diejenige mit dem geringsten Gewicht und wird deshalb zusammen mit dem Knoten E zum Graphen T hinzugefügt.
Mit dem bestehenden Graphen T kann der Knoten C durch die Kanten BC oder EC und der Knoten G durch die Kanten EG oder FG verbunden werden. Unter diesen Kanten ist EC diejenige mit dem geringsten Gewicht und wird deshalb zusammen mit dem Knoten C zum Graphen T hinzugefügt.
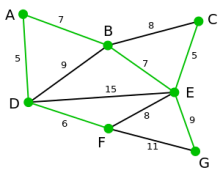
Der verbliebene Knoten G kann durch die Kanten EG oder FG mit dem Graphen T verbunden werden. Da EG unter diesen beiden das geringere Gewicht hat, wird sie zusammen mit dem Knoten G zum Graphen T hinzugefügt
Der Graph T enthält jetzt alle Knoten des Ausgangsgraphen und ist ein minimaler Spannbaum dieses Ausgangsgraphen.

(A2)
Übersetze die Beschreibung aus Aufgabe 1 in Pseudocode.
Pseudocode Prim
Minimal spanning tree:
Hole eine Liste aller Kanten und sortiere sie aufsteigend
Setze einen beliebigen Knoten auf markiert
Wiederhole n-1 mal * Versuche herauszufinden, wie der Algorithmus funktioniert, indem du ihn Schritt für Schritt ausführst.
* Welche Situation muss vermieden werden? Fällt dir dafür eine einfache Lösung ein.
* Beschreibe deinen so gefundenen Algorithmus in einem kurzen Text.
* Vergleiche deine Beschreibung mit den Musterlösung (unten) und bewerte, ob du das Vorgehen richtig nachvollzogen hast.
Wiederhole für jede Kante ka der Liste
Falls Markierung des Startknotens != Markierung des Zielknotens
naechsteKante = ka
brich Schleife ab
Ende-Falls
Ende-Wiederhole
Markiere naechsteKante und lösche sie aus der Liste
Markiere Start- und Zielknoten
Ende Wiederhole

(A3)
Implementiere eine eigene Version des Prim-Algorithmus im Graphentester.
Lösungsvorschlag
List<Knoten> knoten = g.getAlleKnoten();
List<Kante> kanten = g.getAlleKanten();
Collections.sort(kanten);
knoten.get(0).setMarkiert(true);
for(int i = 1; i<knoten.size(); i++) {
Kante ka=null;
for(Kante ka2 : kanten) {
if(ka2.getStart().isMarkiert() != ka2.getZiel().isMarkiert()) {
ka = ka2;
break;
}
}
ka.setMarkiert(true);
kanten.remove(ka);
ka.getStart().setMarkiert(true);
ka.getZiel().setMarkiert(true);
}