Dies ist eine alte Version des Dokuments!
Logische Funktionen finden
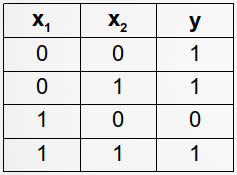
Häufig ist die Funktion als Wertetabelle gegeben, zum Beispiel1)
Ausführlich übersetzt lautet die so definierte logische Funktion von links nach rechts gelesen also:
- Wenn x1 = 0 und x2 = 0, dann ist y = 1.
- Wenn x1 = 0 und x2 = 1, dann ist y = 1.
- Wenn x1 = 1 und x2 = 0, dann ist y = 0.
- Wenn x1 = 1 und x2 = 1, dann ist y = 1.
Wie realisiert man diese Funktion mit den elementaren AND, OR und NOT-Gattern?
Man kann die Wertetabelle auch von recht nach links lesen:
- y=1 wenn x1=0 und x2=0
- y=1 wenn x1=0 und x2=1
- y=0 wenn x1=0 und x2=0
- y=1 wenn x1=1 und x2=1
Wenn man jetzt die Fälle zusammenfasst, in denen y=1 ist, erhält man:
y=1 wenn…
- … x1=0 und x2=0 ODER
- … x1=0 und x2=1 ODER
- … x1=1 und x2=1
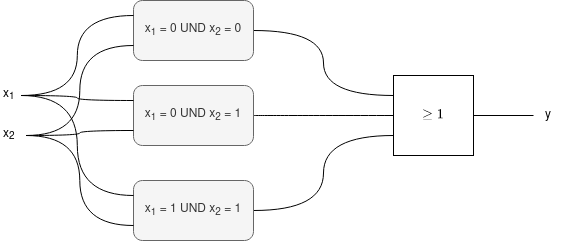
Nun muss man also nur noch für die drei Teilbedingungen die entsprechenden Schaltungen finden und diese mit OR verknüpfen.
y=1 wenn…
- … (¬X1) ∧ (¬X2)
- … (¬X1) ∧ X2
- … X1 ∧ X2
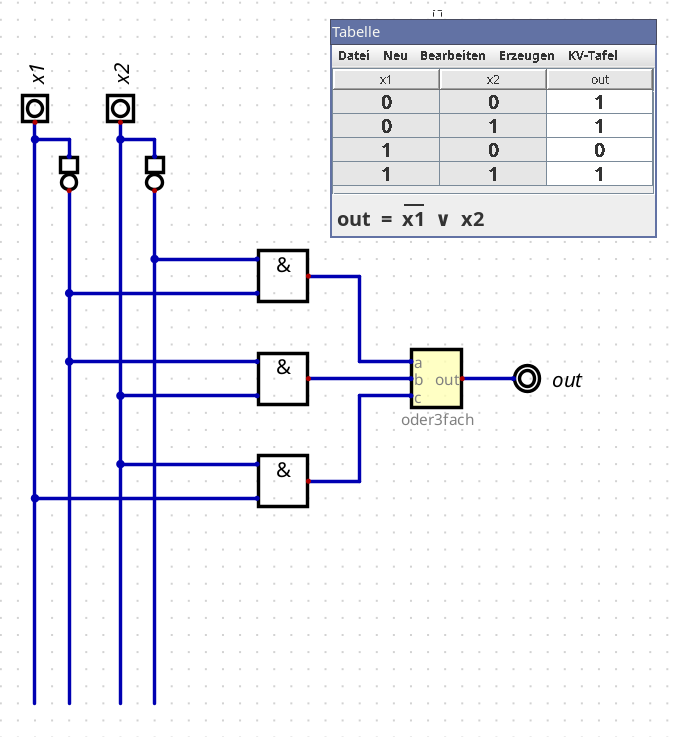
Das kann man ziemlich direkt als Schaltung eintragen:
Schnellanleitung
- Suche alle Zeilen, in denen der Ausgabewert 1 ist
- Bilde für jede dieser Zeilen AND-Terme aus allen Eingabewerten (x-Werten).
- An Stellen, an denen xi=1 ist, bleibt die Variable xi im Term unverändert
- An Stellen, an denen xi=0 ist, muss die Variable xi mit NOT negiert werden
- Verknüpfe die AND-Terme aller Zeilen mit OR
Übungen

(A1)
Finde den Ausdruck für die Logikfunktion und entwerfe die Schaltung im Simulator. Kontrolliere dein Ergebnis anhand der Wertetabelle.
| x0 | x1 | y |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 1 |

(A2)
Vervollständige die untenstehende Tabelle gemäß der Beschreibung. Realisiere jede Funktion yi anschließende als Schaltung in Piiri.
- y0 ist genau dann 1, wenn alle Eingänge 1 sind
- y1 ist genau dann 1, wenn mindestens ein Eingang 1 ist
- y2 ist genau dann 1, wenn alle Eingänge 0 sind
- y3 ist genau dann 1, wenn mindestens ein Eingang 0 ist
- y4 ist genau dann 1, wenn x0=1 und x1=x2=0 ist
- y5 ist genau dann 1, wenn x0=1 und mindestens einer der beiden Eingänge x1 und x2 1 ist.
- y6 ist genau dann 1, wenn x0=1 und genau einer der beiden Eingänge x1 und x2 1 ist.
- y7 ist genau dann 1, wenn die Anzahl der mit 1 belegten Eingänge ungerade ist
- y8 ist genau dann 1, wenn mindestens zwei Eingänge 1 sind
- y9 ist genau dann 1, wenn x0=x1=x2=0 oder x0=x1=x2=1
Finde für y10 und y11 verbale Beschreibungen:
- y10 ist …
- y11 ist …

(A3)
Gegeben sind die Wertetabellen der logischen Funktion f und g:
Finde die Ausdrücke für die Logikfunktionen und entwerfe Schaltungen in Piiri. Kontrolliere dein Ergebnis anhand der Wertetabelle in Piiri.