Logische Funktionen finden
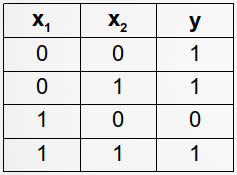
Häufig ist die Funktion als Wertetabelle gegeben, zum Beispiel1)
Ausführlich übersetzt lautet die so definierte logische Funktion von links nach rechts gelesen also:
- Wenn x1 = 0 und x2 = 0, dann ist y = 1.
- Wenn x1 = 0 und x2 = 1, dann ist y = 1.
- Wenn x1 = 1 und x2 = 0, dann ist y = 0.
- Wenn x1 = 1 und x2 = 1, dann ist y = 1.
Wie realisiert man diese Funktion mit den elementaren AND, OR und NOT-Gattern?
Man kann die Wertetabelle auch von recht nach links lesen:
- y=1 wenn x1=0 und x2=0
- y=1 wenn x1=0 und x2=1
- y=0 wenn x1=0 und x2=0
- y=1 wenn x1=1 und x2=1
Wenn man jetzt die Fälle zusammenfasst, in denen y=1 ist, erhält man:
y=1 wenn…
- … x1=0 und x2=0 ODER
- … x1=0 und x2=1 ODER
- … x1=1 und x2=1
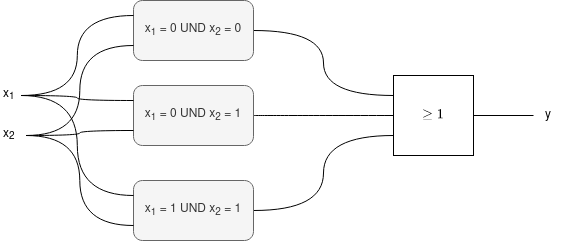
Nun muss man also nur noch für die drei Teilbedingungen die entsprechenden Schaltungen finden und diese mit OR verknüpfen.
y=1 wenn…
- … (¬X1) ∧ (¬X2)
- … (¬X1) ∧ X2
- … X1 ∧ X2
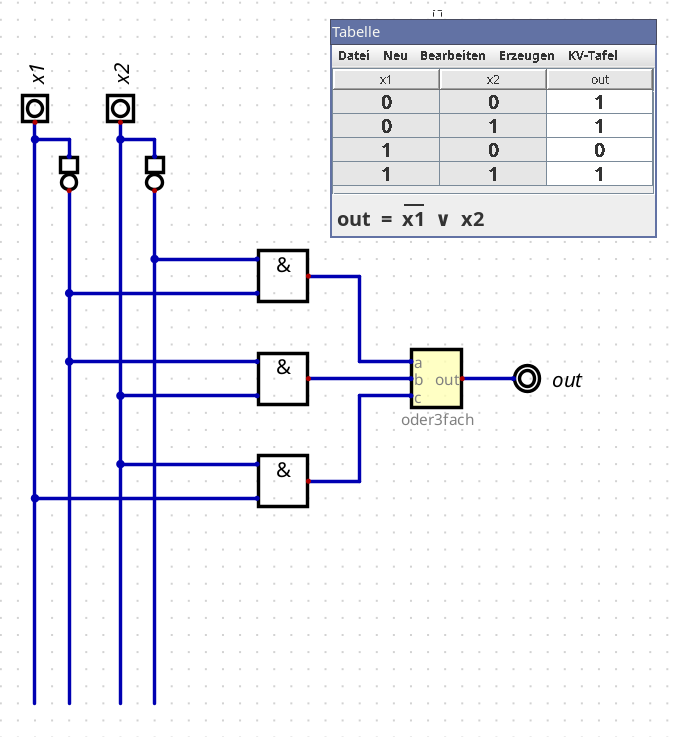
Das kann man ziemlich direkt als Schaltung eintragen:
Schnellanleitung
- Suche alle Zeilen, in denen der Ausgabewert 1 ist
- Bilde für jede dieser Zeilen AND-Terme aus allen Eingabewerten (x-Werten).
- An Stellen, an denen xi=1 ist, bleibt die Variable xi im Term unverändert
- An Stellen, an denen xi=0 ist, muss die Variable xi mit NOT negiert werden
- Verknüpfe die AND-Terme aller Zeilen mit OR
(Hinweis: Das entspricht dem Finden der disjunktiven Normalform)
Übungen

(A1)
Finde den Ausdruck für die Logikfunktion und entwerfe die Schaltung im Simulator. Kontrolliere dein Ergebnis anhand der Wertetabelle.
| x0 | x1 | y |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 1 |

(A2)
Vervollständige die untenstehende Tabelle gemäß der Beschreibung. Realisiere jede Funktion yi anschließende als Schaltung im Simulator
- y0 ist genau dann 1, wenn alle Eingänge 1 sind
- y1 ist genau dann 1, wenn mindestens ein Eingang 1 ist
- y2 ist genau dann 1, wenn alle Eingänge 0 sind
- y3 ist genau dann 1, wenn mindestens ein Eingang 0 ist
- y4 ist genau dann 1, wenn x0=1 und x1=x2=0 ist
- y5 ist genau dann 1, wenn x0=1 und mindestens einer der beiden Eingänge x1 und x2 1 ist.
- y6 ist genau dann 1, wenn x0=1 und genau einer der beiden Eingänge x1 und x2 1 ist.
- y7 ist genau dann 1, wenn die Anzahl der mit 1 belegten Eingänge ungerade ist
- y8 ist genau dann 1, wenn mindestens zwei Eingänge 1 sind
- y9 ist genau dann 1, wenn x0=x1=x2=0 oder x0=x1=x2=1
Finde für y10 und y11 verbale Beschreibungen:
- y10 ist …
- y11 ist …

(A3)
Gegeben sind die Wertetabellen der logischen Funktion f und g:
Finde die Ausdrücke für die Logikfunktionen und entwerfe Schaltungen im Simulator. Kontrolliere dein Ergebnis anhand der Wertetabelle.