Normalformen
Disjunktive Normalform
Die disjunktive Normalform bietet ein Verfahren, mit dem man systematisch einen Logik-Term zu einer Wahrheitstabelle finden kann, bei dem der entstehende Term eine Disjunktion von Konjunktionstermen ist – also eine Oder-Verknüpfung von Und-Verknüpfungen.
Vorgehen:
Die disjunktive Normalform erhält man, indem man alle Minterme durch Oder-Verknüpfungen verbindet.
Beispiel:
- Für jede Zeile, die "wahr" ist, bildet man den Minterm mit "und". Alle "falsch" Werte werden dabei einfach negiert.
- Alle so gefundenen Zeilen verknüpft man mit "oder"
Die disjunktive Normalform für die Wahrheitstafel im Beispiel ist also $(\lnot x_1 \land \lnot x_2) \lor (x_1 \land \lnot x_2)$.
Konjunktive Normalform
Die konjunktive Normalform bietet ein Verfahren, mit dem man systematisch einen Logik-Term zu einer Wahrheitstabelle finden kann, bei dem der entstehende Term eine Konjunktion von Disjunktionstermen ist – also eine Und-Verknüpfung von Oder-Verknüpfungen.
Vorgehen:
Die konjunktive Normalform erhält man, indem man alle Maxterme durch Und-Verknüpfungen verbindet.
Beispiel:
- Für jede Zeile, die "falsch" ist, bildet man den Maxterm mit "oder". Alle "wahr" Werte werden dabei einfach negiert.
- Alle so gefundenen Zeilen verknüpft man mit "und"
Eine konjunktive Normalform für die Wahrheitstafel im Beispiel ist also $(x_1 \lor \lnot x_2) \land (\lnot x_1 \lor \lnot x_2)$.

(A1)
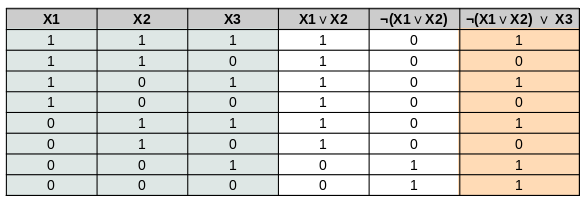
Stelle zum Term $(\lnot(x_1 \lor x_2) \lor x_3)$ die Wahrheitstafel auf und ermittle daraus die DNF und eine KNF. Versuche dann DNF und KNF durch Umformungen des Terms zu erhalten - welche Rechenregeln verwendest du dabei?
Lösungshinweis 1 - Wahrheitstabelle

(A2)
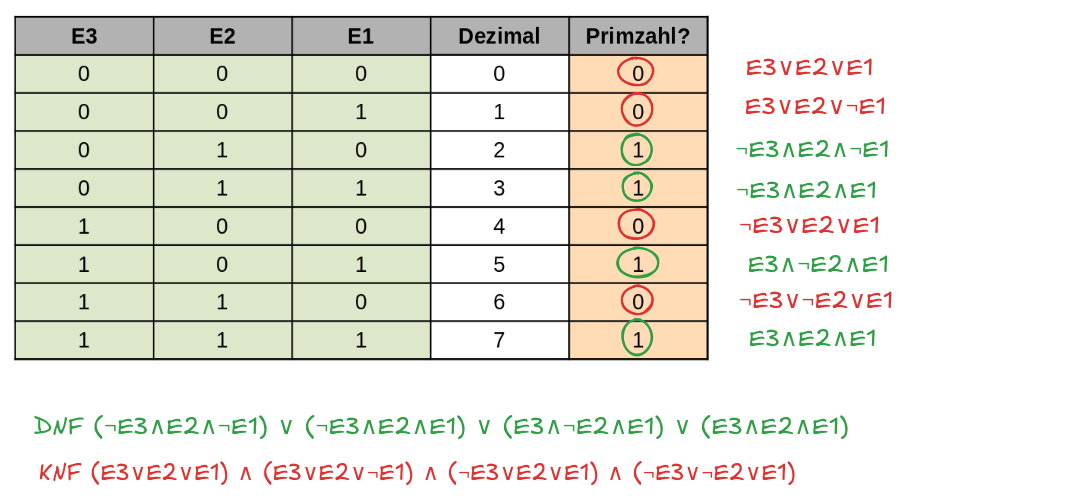
Gesucht ist eine boolesche Funktion mit drei Variablen E1, E2 und E3, deren Ausgang A genau dann den Wert TRUE annimmt, wenn die Dualzahl[E3 E2 E1]2 eine Primzahl ist.
- Ermittle die DNF der Funktion.
- Vereinfache die DNF der Funktion so weit wie möglich.
- Erstelle die KNF der Funktion.
- Vereinfache die KNF der Funktion so weit wie möglich.
- Überprüfe ob die beiden vereinfachten Terme aus DNF und KNF zum gleichen Resultat führen.
Diese Seite ist sehr stark an das Material auf https://inf-schule.de/rechner/digitaltechnik/Schaltnetze/Fachkonzept_Normalform angelehnt, das unter einer CC-BY-SA Lizenz veröffentlicht ist.